10.4 그래프의 탐색
● 그래프 탐색: 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
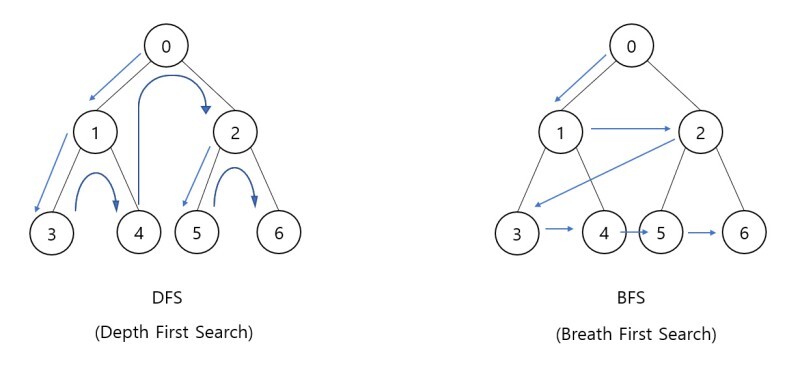
- 깊이 우선 탐색(DFS: depth first search): 시작 정점에서 한 방향으로 계속 가다가 더 이상 갈 수 없게 되면
가장 가까운 갈림길로 돌아와서 다른 방향으로 탐색하는 순회 방법
- 너비 우선 탐색(BFS: breath first search): 시작 정점으로부터 가까운 정점을 먼저 방문하고
멀리 떨어진 정점을 나중에 방문하는 순회 방법
10.5 깊이 우선 탐색
- 시작 정점 v부터 방문한 정점을 표시하고, 인접한 정점들 중에서 아직 방문하지 않은 정점 u를 선택
- 방문하지 않은 정점이 없으면 탐색 종료
- 아직 방문하지 않은 정점 u가 있다면 그 u를 새로운 시작 정점으로 하여 DFS를 재수행 (순환 알고리즘)
● 깊이 우선 탐색의 구현(인접 행렬 버전)
- 순환 호출 or 명시적인 스택을 사용하여 인접한 정점들을 스택에 저장 후 꺼내기
- 방문여부를 배열 vistied에 기록. 방문 후에는 TRUE로 변경
- adj_mat[v][w] 값이 1이면 정점 v와 w는 인접한 것, 정점 w가 아직 방문되지 않았으면 정점 w에서 DFS 재실행
int visited[MAX_VERTICES];
void dfs_mat(GraphType *g, int v){
int w;
visited[v] = TRUE;
printf("정점 %d -> ",v);
for(w=0; w<g->n;w++){
if(g->adj_mat[v][w] && !visited[w]){
dfs_mat(g,w);
}
}
}
● 깊이 우선 탐색의 구현(인접 리스트 버전)
- 마찬가지로 순환호출
- 정점 v에 대해 인접 정점들을 w= w->link로 탐색하고, 방문되지 않은 정점이 있으면 해당 정점에서 DFS 재실행
void dfs_list(GraphType *g,int v){
GraphNode *w;
visited[v]= TRUE;
printf("정점 %d -> ",v);
for(w=g->adj_list[v];w;w=w->link){
if(!visited[w->vertex]){
dfs_list(g,w->vertex);
}
}
}
● 깊이 우선 탐색의 구현(인접 리스트 + 명시적인 스택)
- 스택을 하나 생성하여 시작 정점을 스택에 넣고, 정점의 인접 정점들을 스택에 추가.
- 스택이 빌 때까지 인접 정점들을 하나씩 꺼내서 다시 인접 정점들을 탐색
- 탐색 중 방문하지 않은 노드가 있으면 스택에 push
void dfs_iterative(GraphType *g,int v){
StackType *s = (StackType*)malloc(sizeof(StackType));
GraphNode *w;
push(s,v);
while(!is_empty(s)){
v=pop(s);
if(visited[v]!=TRUE){
visited[v]=TRUE;
printf("정점 %d -> ",v);
for(w=g->adj_list[v];w;w=w->link){
if(!visited[w->vertex]){
push(s,w->vertex);
}
}
}
}
}
● 깊이 우선 탐색의 분석
- 모든 간선을 조사하므로 정점의 수가 n, 간선의 수가 e인 그래프에 대해
인접 리스트: O(n+e) 인접 행렬: O(n^2)의 시간복잡도를 가진다.
즉, 희소 그래프일 경우 DFS는 인접 리스트 사용이 더 유리함을 뜻한다.
♠ 385p Quiz
01 0 -> 1 ->2 -> 4 -> 3
10.6 너비 우선 탐색
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문
- 큐에서 정점을 꺼내서 정점을 방문하고 방문하지 않은 인접 정점들을 큐에 추가한다.
- 큐가 소진될 때까지 동일한 코드 반복
● 너비 우선 탐색의 구현(인접 행렬 버전)
- 큐를 사용하여 정점을 enqueue하고 인접 정점 탐색 후 방문하지 않은 정점이 있으면 방문 후 enqueue
- 방문여부를 배열 vistied에 기록. 방문 후에는 TRUE로 변경
- adj_mat[v][w] 값이 1이면 정점 v와 w는 인접한 것, 정점 w가 아직 방문되지 않았으면 방문 후 enqueue
void bfs_mat(GraphType *g,int v){
int w;
QueueType *q = (QueueType*)malloc(sizeof(QueueType));
init_queue(q);
visited[v]= TRUE;
printf("%d 방문 -> ",v);
enqueue(q,v);
while(!is_empty(q)){
v= dequeue(q);
for(w=0;w<g->n;w++){
if(g->adj_mat[v][w] && !visited[w]){
visited[w] = TRUE;
printf("%d 방문 -> ",w);
enqueue(q,w);
}
}
}
}
● 너비 우선 탐색의 구현(인접 리스트 버전)
- 큐를 생성하여 첫 정점을 enqueue하고, 큐에서 하나씩 dequeue 하면서 인접 정점들을 방문
- 탐색 중 방문하지 않은 정점이 있으면 queue
void bfs_list(GraphType *g,int v){
GraphNode *w;
QueueType *q=(QueueType*)malloc(sizeof(QueueType));
init_queue(q);
visited[v] = TRUE;
printf("%d 방문 -> ",v);
enqueue(q,v);
while(!is_empty(q)){
v=dequeue(q);
for(w=g->adj_list[v];w;w=w->link){
if(!visited[w->vertex]==TRUE){
visited[w->vertex] = TRUE;
printf("%d 방문 -> ",w->vertex);
enqueue(q,w->vertex);
}
}
}
}
● 너비 우선 탐색의 분석
- 정점의 수가 n, 간선의 수가 e인 그래프에 대해
인접 리스트: O(n+e) 인접 행렬: O(n^2) 의 시간복잡도를 가진다.
즉, 희소 그래프일 경우 DFS는 인접 리스트 사용이 더 유리함을 뜻한다.
♠ 391p Quiz
01 2 -> 1-> 0 -> 4 -> 3
큐 : 2 -> 1, 0 -> 0, 4 - > 4, 3 -> 3 -> empty
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter11. 그래프 II (1) (0) | 2023.12.13 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 10강 (0) | 2023.12.12 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter10. 그래프 I (1) (1) | 2023.12.08 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 9강 (1) | 2023.12.04 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter9. 우선순위 큐 (2) (1) | 2023.12.02 |
