12.1 정렬이란?
● 정렬: 대상을 크기순으로 오름차순이나 내림차순으로 나열하는 것(키 값을 기준으로)
- 레코드: 정렬시켜야 할 대상
- 필드: 레코드의 구성단위 ex) 학생이라는 레코드의 필드는 이름, 학번, 주소, 등
- 키(key): 레코드와 레코드를 식별해 주는 역할을 하는 필드 ex) 학번
각 상황에서 가장 효율적인 정렬 알고리즘을 선택하여야 함
효율성의 기준 = 비교 연산의 횟수 + 이동 연산의 횟수
● 효율성과 복잡성
단순하지만 비효율적인 정렬 알고리즘 (자료 개수가 적을 때 사용) - 삽입 정렬, 선택 정렬, 버블 정렬 등
복잡하지만 효율적인 정렬 알고리즘 - 퀵 정렬, 히프 정렬, 합병 정렬, 기수 정렬, 권정열 등
● 내부와 외부 정렬
내부 정렬 - 정렬 전 모든 데이터가 메인 메모리에 올라와 있는 정렬
외부 정렬 - 외부 기억 장치에 대부분의 데이터가 있고 일부만 메모리에 올려놓은 상태에서 정렬
● 안정성
안정성: 동일한 키값을 갖는 레코드가 여러 개 존재할 떄, 레코드들의 상대적인 위치가 정렬 후에도 유지됨
- 상대적 위치가 유지되지 않으면 안정하지 않다 = 안정성이 낮다
- 안정성을 충족하는 정렬: 삽입 정렬, 버블 정렬, 합병 정렬 등
이하 정렬들은 숫자 필드만 가지고 있는 레코드이다.
12.1 선택 정렬
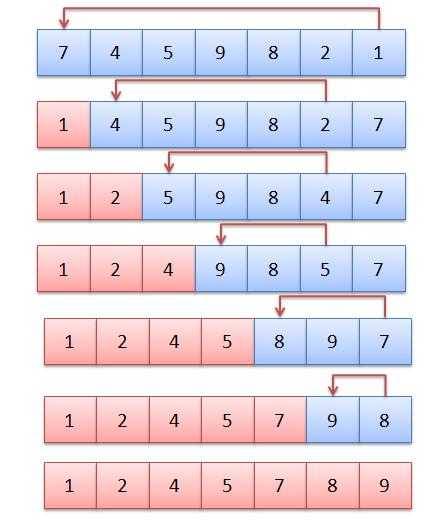
● 선택 정렬의 원리
방법 1) 왼쪽 리스트는 비어 있고, 오른쪽 리스트는 정렬되지 않은 숫자들이 들어 있을 때
오른쪽 리스트에서 가장 작은 숫자를 선택하여 왼쪽 리스트로 이동하는 작업을 오른쪽 리스트가 공백상태가 될 때까지 반복
방법 2) 입력 배열과 크기가 같은 추가적인 배열이 필요하기 때문에, 메모리 절약을 위해 한 배열 내에서 정렬
- 입력 배열에서 최솟값을 발견한 다음, 이 최소값을 배열의 첫 번째 요소와 교환
- 첫번째 요소를 제외한 나머지 요소들 중 가장 작은 값을 선택하고 이를 두 번째 요소와 교환
- 위 절차를 (입력 개수 -1)만큼 반복
● 선택 정렬의 알고리즘, 전체 프로그램
void selection_sort(int list[],int n){
int i,j,least,temp;
for(i=0;i<n-1;i++){
least = i;
for(j=i+1;j<n;j++){
if(list[j]<list[least]) least =j;
}
SWAP(list[i],list[least],temp);
}
}외부 for문: n의 개수만큼 1씩 커지면서 반복 // n-2까지 정렬 돼있으면 n-1이 젤 큰 값이기 때문에 n-2까지만 i 변화
내부 for문: i까지는 정렬된 레코드가 들어있으므로 i+1부터 least 갱신
swap: 이동 3번 수행
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10
#define SWAP(x,y,t) ( (t)=(x), (x)=(y), (y)=(t))
int list[MAX_SIZE];
int n;
void selection_sort(int list[],int n){
int i,j,least,temp;
for(i=0;i<n-1;i++){
least = i;
for(j=i+1;j<n;j++){
if(list[j]<list[least]) least =j;
}
SWAP(list[i],list[least],temp);
}
}
int main(){
int i;
n =MAX_SIZE;
srand(time(NULL));
for(i=0; i<n; i++){
list[i] = rand() %100;
}
selection_sort(list,n);
for(i=0; i<n; i++){
printf("%d ",list[i]);
}
printf("\n");
return 0;
}
● 선택 정렬의 분석
- 비교연산
외부루프 n-1번 실행
내부루프 0에서 n-2까지 변하는 i에 대해 (n-1) -i 번 수행
∴ (n-1) + (n-2) +... + 1 = n(n-1)/2 = O(n^2)
- 이동 연산
SWAP()에서의 3번의 이동을 외부 루프만큼 반복
∴ 3(n-1)
* 자료가 정렬된 경우 불필요하게 자기 자신과의 이동하는 것 방지
if(i != least)
SWAP(list[i], list[least], temp);
최솟값이 자기 자신이면 swap을 수행하지 않고 최소값이 자기 자신이 아닐 때만 수행
- 안정성
키 값이 같은 레코드가 있는 경우 상대적인 위치가 변경될 수 있기에 안정성이 만족되지 않는다.
♠ 450p Quiz
01
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 4 | 9 | 7 | 6 |
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 4 | 6 | 7 | 9 |
02 1 2 5 3 3 6이라는 배열을 정렬할 때, 3이 5와 교체되어 1 2 3 3 5 6과 같이 정렬된다.
12.3 삽입 정렬
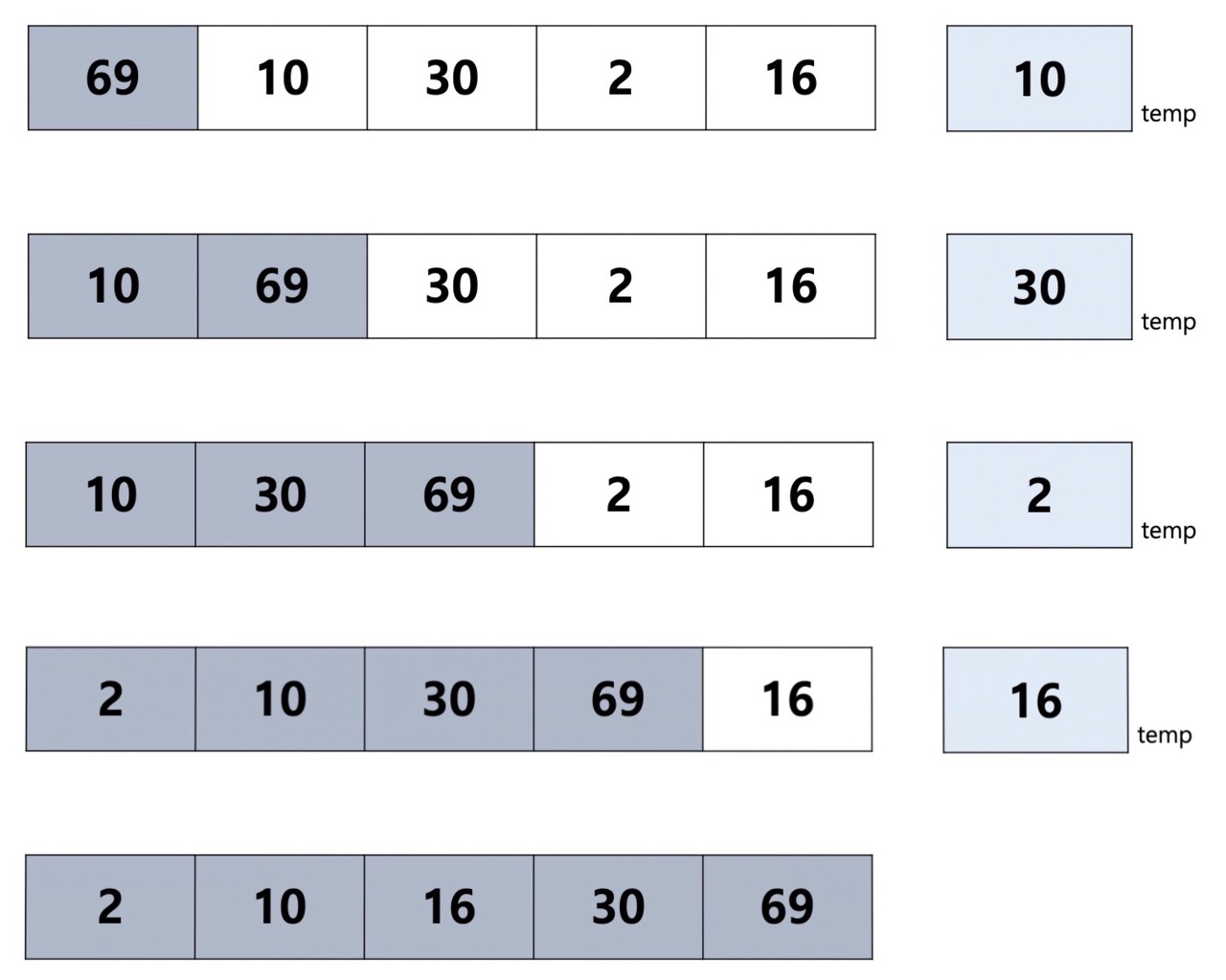
● 삽입 정렬의 원리 및 c언어 구현
- 레코드 개수 크기만큼의 배열 안에서 정렬하며 선택정렬과 마찬가지로 정렬된 부분과 정렬되지 않은 부분으로 나뉜다.
- 정렬되지 않은 부분의 가장 작은 숫자를 선택해 정렬된 부분의 뒤에서부터 차례대로 비교하여 삽입될 위치를 정하여 삽입
- 정렬된 부분에 삽입이 이루어지면 정렬된 부분의 크기는 1 증가
- 정렬되지 않은 부분이 빌 때까지 위 과정을 반복
void insertion_sort(int list[], int n){
int i, j, key;
for(i=1; i<n; i++){ // 두번째 레코드부터 정렬시작
key = list[i];
for(j=i-1;j>=0&&list[j]>key;j--){//정렬된 부분의 끝에서부터 key보다 클 때까지 감소
list[j+1] = list[j];
}
list[j+1] = key;
}
}
● 삽입 정렬의 복잡도 분석
- 정렬된 자료 비교연산
외부 루프가 n-1번 실행될 동안 1번의 비교연산 수행
∴ n-1
- 정렬된 자료 이동연산
외부 루프가 n-1번 실행될동안 2번의 이동연산 수행
∴ 2(n-1)
- 정렬되지 않은 자료 비교연산
외부 루프가 n-1번 실행될동안 반복마다 i번의 비교연산 수행
∴ 1+2+...+(n-1) = n(n-1)/2 = O(n^2)
- 정렬되지 않은 자료 이동연산
외부 루프가 n-1번 실행될동안 반복마다 i+2번의 이동연산 수행
∴ n(n-1)/2 + 2(n-1) = (n^2 +3n -4) /2 = O(n^2)
- 비교적 많은 이동연산을 수행해야 하므로 레코드 양이 많고 레코드 크기가 큰 경우 부적합
- 대부분의 레코드가 이미 정렬되어 있는 경우에 매우 효율적
♠ 455p Quiz
01 3 7 9 4 1 6
3 4 7 9 1 6
1 3 4 7 9 6
1 3 4 6 7 9
02 뒤쪽 레코드를 앞으로 옮기는 이동연산인데 key가 정렬된 부분의 레코드보다 '작을 때만'
이동연산을 수행하기 때문에 같은 경우에는 이동연산이 수행되지 않기 때문에 안정적이다.
12.4 버블 정렬
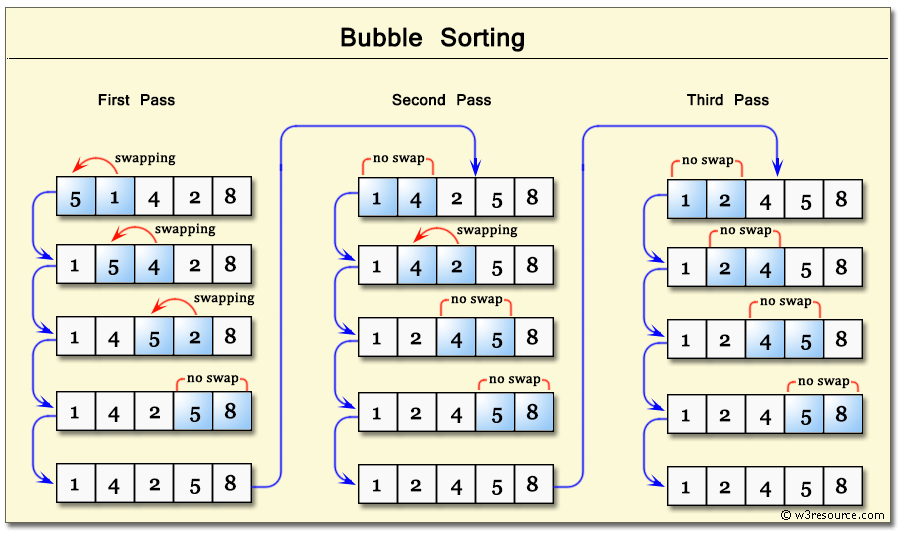
● 버블 정렬의 원리 및 c언어 구현
- 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환하는 비교-교환과정을
리스트의 왼쪽 끝에서 오른쪽 끝까지 진행
- 가장 오른쪽 끝부터 정렬이 완료된 부분이 되고 한 번의 pass를 거치고 나면 정렬된 부분의 크기도 1 증가
- 왼쪽부터 정렬되지 않은 부분이 없을 때까지 위 과정을 반복
void bubble_sort(int list[], int n){
int i, j, temp;
for(i = n-1; i>0; i--){//한번의 pass마다 정렬된 부분의 크기가 1감소
for(j =0; j<i; j++){//정렬되지 않은 부분이 없을 때까지 = i전까지
if(list[j]>list[j+1]){
SWAP(list[j],list[j+1],temp);
}
}
}
}j=0부터 j= i-1까지 정렬되지 않은 부분에서 교환을 수행한다. i는 하나의 pass가 지날 때마다 크기가 1씩 감소한다.
● 버블 정렬의 복잡도 분석
- 비교 연산
버블 정렬은 최선, 평균, 최악의 어떠한 경우에도 항상 일정하고 다음과 같다.
∴ n-1∑i=1 i = n(n-1)/2 = O(n^2)
- 이동 연산
비교 연산마다 SWAP을 수행하기에 SWAP에 이동연산이 3번 포함되므로
∴ 3* 비교연산 = O(n^2)
- 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환이 일어나기 때문에
우수한 단순성에 비해 매우 비효율적이어서 거의 사용되지 않음
♠ 458p Quiz
01 3 7 4 9 1 6
3 7 4 1 6 9
3 4 1 6 7 9
3 1 4 6 7 9
1 3 4 6 7 9
02 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환이 일어나고
자료가 정렬된 경우에도 불필요하게 이동 연산이 수행되기 때문
12.5 쉘 정렬
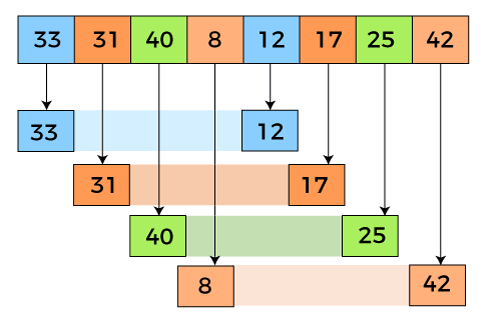
● 쉘 정렬의 원리
삽입 정렬의 보완버전
- 삽입 정렬은 요소들이 삽입될 때, 이웃한 위치로만 이동하여 상당히 많은 이동연산이 요구됨
- 쉘 정렬은 리스트를 gap을 기준으로 분류하여 연속적이지 않은 여러 개의 부분 리스트로 만들어
- 각 부분 리스트를 정렬시키고 나면 더 작은 gap으로 부분리스트를 만든 뒤 알고리즘 반복
- 위 과정을 부분 리스트의 개수가 1개가 될 때까지 반복
*마지막 스텝의 gap의 값은 1이다.
● 쉘 정렬의 구현
void inc_insertion_sort(int list[],int first, int last, int gap){
int i, j, key;
for(i = first + gap; i<=last; i= i+gap){
key = list[i];
for(j=i-gap;j>=first && key<list[j]; j = j-gap){
list[j+gap] = list[j];
}
list[j+gap] =key;
}
}- 삽입 정렬과 같은 메커니즘
- 삽입 정렬에서 한 칸씩 움직이던 비교 및 이동 연산이 쉘 정렬에서는 gap만큼 움직임
void shell_sort(int list[],int n){
int i,gap;
for(gap = n/2; gap>0; gap = gap/2){
if((gap%2)==0) gap++;
for(i =0; i<gap; i++){
inc_insertion_sort(list,i,n-1,gap);
}
}
}- gap이 1이 될 때까지 gap을 1/2로 줄이면서 반복'
- 간격이 짝수이면 1을 더하는 것이 더 좋은 것으로 분석되어 코드에 반영 -> if( (gap%2) ==0 ) gap++;
● 쉘 정렬의 분석
- 연속적이지 않은 부분 리스트에서 gap만큼의 거리를 이동하기 때문에 교환되는 아이템들이 삽입 정렬보다
최종 위치에 더 가까이 있을 가능성이 높다.
- 부분리스트가 이미 어느 정도 정렬된 상태이기 때문에 부분 리스트가 1개일 때의 삽입 정렬은 비교적 빠르게 수행된다.
최악의 경우 O(n^2) 평균적인 경우 O(n^1.5)
♠ 462p Quiz
01 4 8 5 7 6 2 1 3
1 8 5 4 6 2 7 3
1 6 5 4 8 2 7 3
1 3 5 4 6 2 7 8
1 3 2 4 6 5 7 8 // gap 3
1 2 3 4 6 5 7 8
1 2 3 4 5 6 7 8 // gap 1
02 O(n^2)인 삽입 정렬은 100,000,000, O(n^1.5)인 쉘 정렬은 1,000,000 이므로 100배 빠르다.
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 12강 (1) | 2024.01.07 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] Chapter12. 정렬 (2) (0) | 2024.01.04 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 11강 (1) | 2023.12.17 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter11. 그래프 II (2) (0) | 2023.12.15 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter11. 그래프 II (1) (0) | 2023.12.13 |
