13.4 이진 탐색 트리
이진 탐색은 자료들이 배열에 저장되어 있어 삽입과 삭제가 힘들다는 단점 존재
이진 탐색 트리는 삽입, 삭제가 빈번한 상황에서 사용
- 이진 탐색 트리는 트리가 균형 트리 일 때 O(log2n)의 시간 복잡도를, 균형 트리가 아닐 때는
최악의 경우 O(n)의 시간복잡도를 가짐
| 알고리즘 | 최악 | 평균 | ||
| 탐색 | 삽입 | 탐색 | 삽입 | |
| 순차 탐색(정렬x) | N | N | N/2 | N |
| 이진 탐색(정렬o) | logN | N | logN | N/2 |
| 이진 탐색 트리 | N | N | logN | logN |
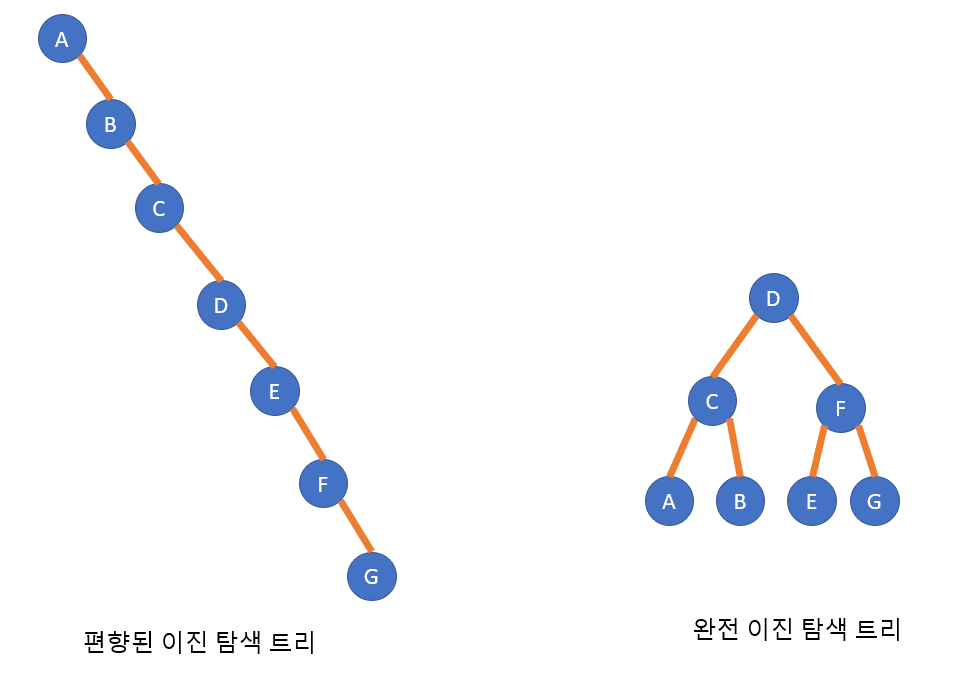
모든 항목이 균일하게 탐색된다는 가정 하에 평균 비교 횟수를 비교
좌측 트리와 같은 편향된 경사 트리는 (1+2+3+4+5+6+7)/7 = 4
우측 트리와 같은 균형트리는 (1+2+2+3+3+3+3)/7 = 2.4
따라서 이진 탐색 트리에서는 균형을 유지하는 것이 중요
13.5 AVL 트리
AVL트리: 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 차이가 1 이하인 이진 탐색 트리
- 트리가 삽입, 삭제 등으로 비균형 상태가 되면 스스로 노드를 재배치하여 균형 상태로 만듦
- 균형 트리가 항상 보장되어 O(logn)시간안에 탐색, 삽입, 삭제 가능
균형 인수(balance factor): (왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이)
균형 인수가 ±1이하면 AVL 트리
● AVL 트리의 탐색 연산
일반적인 이진 탐색 트리와 같이 O(log2n)의 시간 복잡도를 가진다.
● AVL 트리의 삽입 연산
- 삽입되는 위치 ~ 루트 경로에 있는 조상 노드들의 균형 인수에 영향을 줄 수 있기에
삽입 연산 이후 불균형 상태로 변한 가장 가까운 조상 노드, 즉 균형 인수가 ±2가 된 가장 가까운 조상 노드의
서브 트리들에 대하여 재배치하여 균형 상태로 만들어야 한다.
재배치: 새로운 노드~ 균형 인수가 ±2가 된 가장 가까운 조상 노드까지를 회전
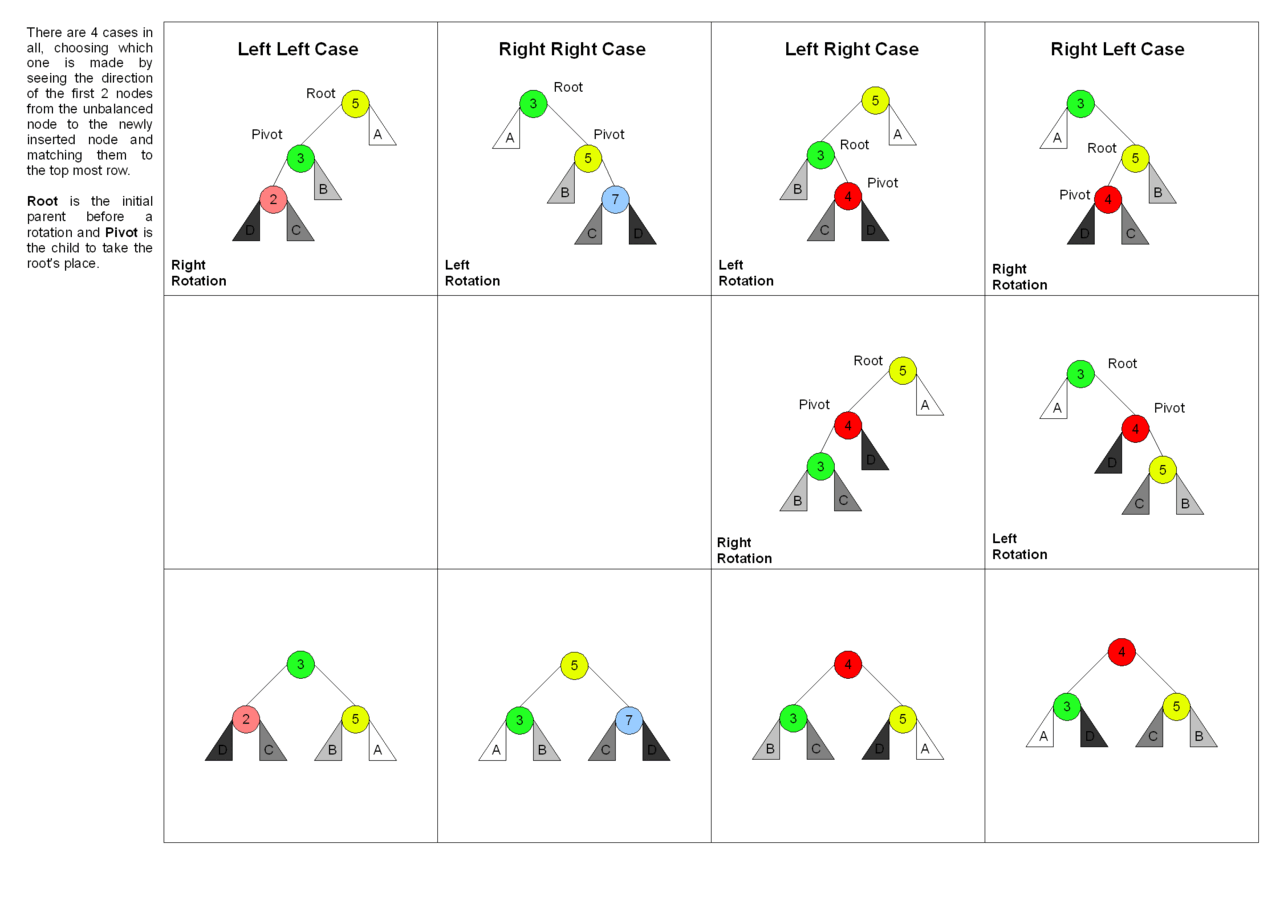
● AVL 트리 예제
삽입을 통해 트리의 균형이 깨지게 되면 균형을 이루기 위해 LL, LR, RL, RR 회전 중 상황에 맞는 회전을 선택한다.
이들 회전은 모두 새로 삽입된 노드로부터 ±2의 균형 인수를 가지는 가장 가까운 조상 노드에 대하여 이루어진다.
● AVL 트리의 정의
typedef struct AVLNode{
int key;
struct AVLNode *left;
struct AVLNode *right;
}AVLNode;AVL 트리도 이진 탐색 트리의 일종
● rotate_right(), rotate_left() 함수 구현
AVLNode *rotate_right(AVLNode *parent){
AVLNode* child = parent -> left;
parent->left = child-> right;
child-> right = parent;
return child;
}
AVLNode *rotate_left(AVLNode *parent){
AVLNode* child = parent -> right;
parent->right = child -> left;
child-> left = parent;
return child;
}부모 노드의 왼쪽 노드를 자식 노드의 오른쪽 노드로 바꾸고, 자식 노드의 오른쪽 노드를 기존 부모노드로 둔 뒤
자식 노드를 return하면 오른쪽으로 회전 된다.
● get_height(), get_balance() 함수 구현
int get_height(AVLNode *node){
int height = 0;
if(node !=NULL){
height = 1+ max(get_height(node->left),get_height(node->right));
}
return height;
}
int get_balanced(AVLNode *node){
if(node ==NULL) return 0;
return get_height(node->left) - get_height(node->right);
}
● 새로운 노드 추가 함수
AVLNode* insert(AVLNode *node, int key){
if(node ==NULL) return (create_node(key));
if(key< node->key){
node->left = insert(node->left,key);
}
else if(key> node->key){
node->right = insert(node->right,key);
}
else return node;
int balance = get_balanced(node);
// balance >1 이면 왼쪽 자식, balance <-1 이면 오른쪽 자식에 삽입되었고
// key<node->left->key 이면 자식의 왼쪽에 추가 key>node->right->key 이면 자식의 오른쪽에 추가
if(balance >1 && key< node->left->key){
return rotate_right(node);
} // LL
if(balance <-1 && key> node->right->key){
return rotate_left(node);
} //RR
if(balance >1 && key> node->left->key){
node->left = rotate_left(node->left);
return rotate_right(node);
} //LR
if(balance <-1 && key< node->right->key){
node->right = rotate_right(node->right);
return rotate_left(node);
} //RL
return node;
}주석참고
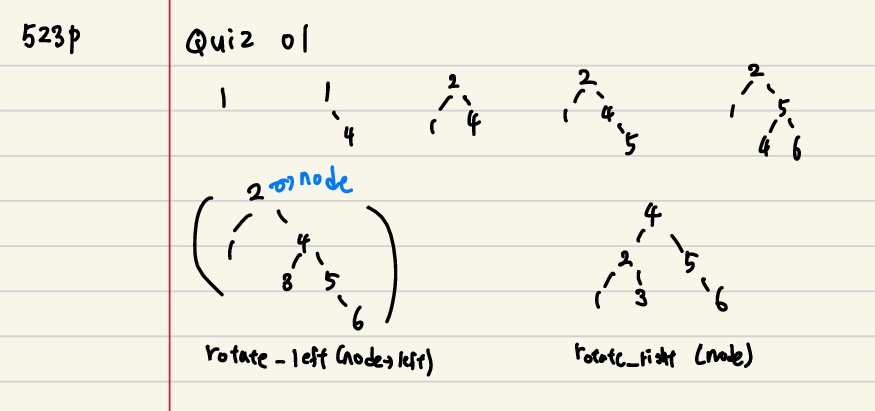
♠ 523p Quiz
01
13.6 2-3 트리
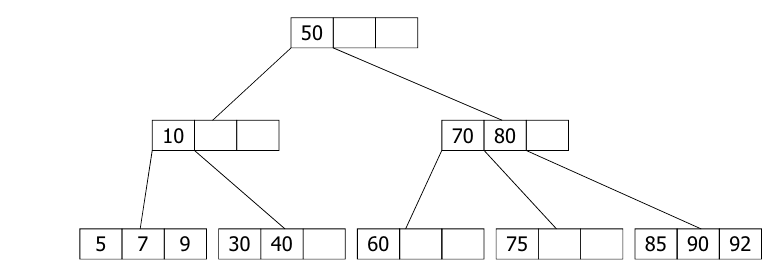
● 2-3 트리: 차수가 2 또는 3인 노드를 가지는 트리
- 삽입이나 삭제 연산이 AVL트리보다 간단
- 2-노드는 하나의 데이터 k1와 두개의 자식 노드를, 3-노드는 두개의 데이터 k1,k2와 3개의 자식노드를 가짐
- 왼쪽 서브트리는 k1보다 작은 값, 중간 서브트리는 k1보다 크고 k2보다 작은 값, 오른쪽 서브트리는 k2보다 큰 값
● 2-3 트리의 탐색 연산
노드가 2-노드인지 3-노드인지에 따라 탐색을 각각 진행
2-노드면 탐색 key가 현재 노드의 key보다 작다면 왼쪽 서버트리를, 크다면 오른쪽 서브트리를 순환탐색
● 2-3 트리의 삽입 연산
노드는 2개의 데이터값을 저장. 저장 가능할 때까지 데이터 추가, 더 이상 저장할 장소가 없을 땐 노드 분리
중간 값을 한레벨 위로 올리고 제일 작은 값을 왼쪽 노드, 큰 값을 오른쪽 노드로 만듦
노드 분리되는 상황
case1. 단말 노드를 분리
- 부모노드가 2-노드: 중간값이 부모노드로 올라가고 작은 값과 큰 값은 새로운 노드로 분리
- 부모노드가 이미 2개의 데이터를 가진 3-노드: 부모 노드가 다시 재분리 되어 case2 적용
case2. 비단말 노드를 분리
- 중간 값을 다시 부모 노드로 올려보내고 작은 값과 큰 값은 새로운 노드로 분리
- 부모 노드에 올라간 추가 노드를 받을 공간이 없다면 계속 상위 부모 노드로 순환 ( bottom up )
case3. 루트 노드를 분리
- bottom up이 진행되다가 루트 노드에 도달하여 루트 노드를 분리하게 되면 트리의 노드 1 증가
- 중간값이 올라가서 만든 새로운 노드는 새로운 루트 노드가 됨
case3에서만 트리의 높이가 1 증가
♠ 528p Quiz
01
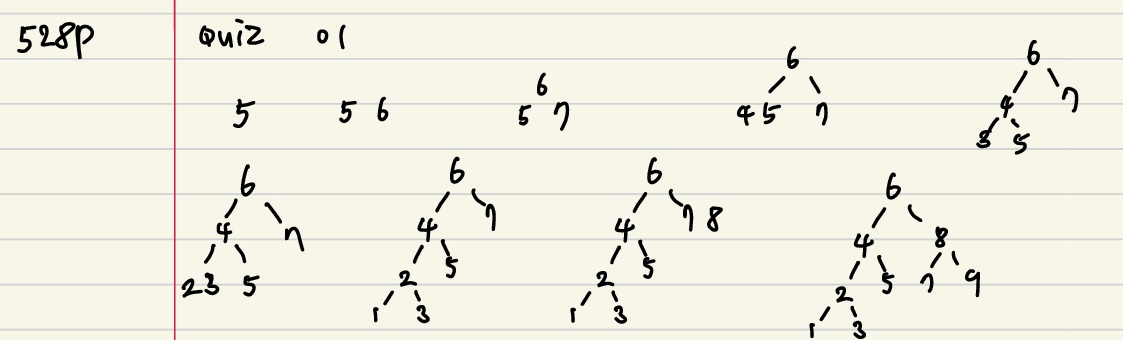
13.7 2-3-4 트리

● 2-3-4 트리: 차수가 2 또는 3 또는 4인 노드를 가지는 트리, 2-3 트리의 확장 버전
- 4-노드는 4개의 자식을 가질 수 있으며 3개의 데이터를 가질 수 있다.
3개의 데이터를 크기 순으로 small, middle, large라고 하면
1. small 보다 작은 값은 첫번째 자식 노드
2. small보다 크고 middle보다 작은 값은 두번째 자식 노드
3. middle보다 크고 large보다 큰 값은 세번째 자식 노드
4. large보다 큰 값은 네번째 자식 노드
● 2-3-4 트리의 삽입 연산
- 삽입하는 단말노드가 4-노드이면 후진분할이 일어나는데, 이를 방지하기 위해
삽입노드를 찾는 순회 과정에서 4-노드를 만나면 미리 분할을 수행해놓는다.
이는 2-3트리와 달리 루트에서 단말 노드로 한번만 순회하여 삽입이나 삭제가 가능하게 한다.
순회 중 4-노드를 만난 경우
case1. 4-노드가 루트인 경우
- 4-노드의 중간값을 상위 레벨로 올려 새로운 노드를 만들며 해당 노드가 새로운 루트 노드가 된다.
case2. 4-노드의 부모가 2-노드인 경우
case3. 4-노드의 부모가 3-노드인 경우
- 4-노드의 중간값을 상위 레벨로 올려 위치하게 한 뒤, 작은 값과 큰 값은 적절한 위치에 자식 노드로 분리한다.
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter14. 해싱 (1) (0) | 2024.01.20 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 13강 (0) | 2024.01.20 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter13. 탐색 (1) (1) | 2024.01.08 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 12강 (1) | 2024.01.07 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter12. 정렬 (2) (0) | 2024.01.04 |
