14.1 해싱이란?
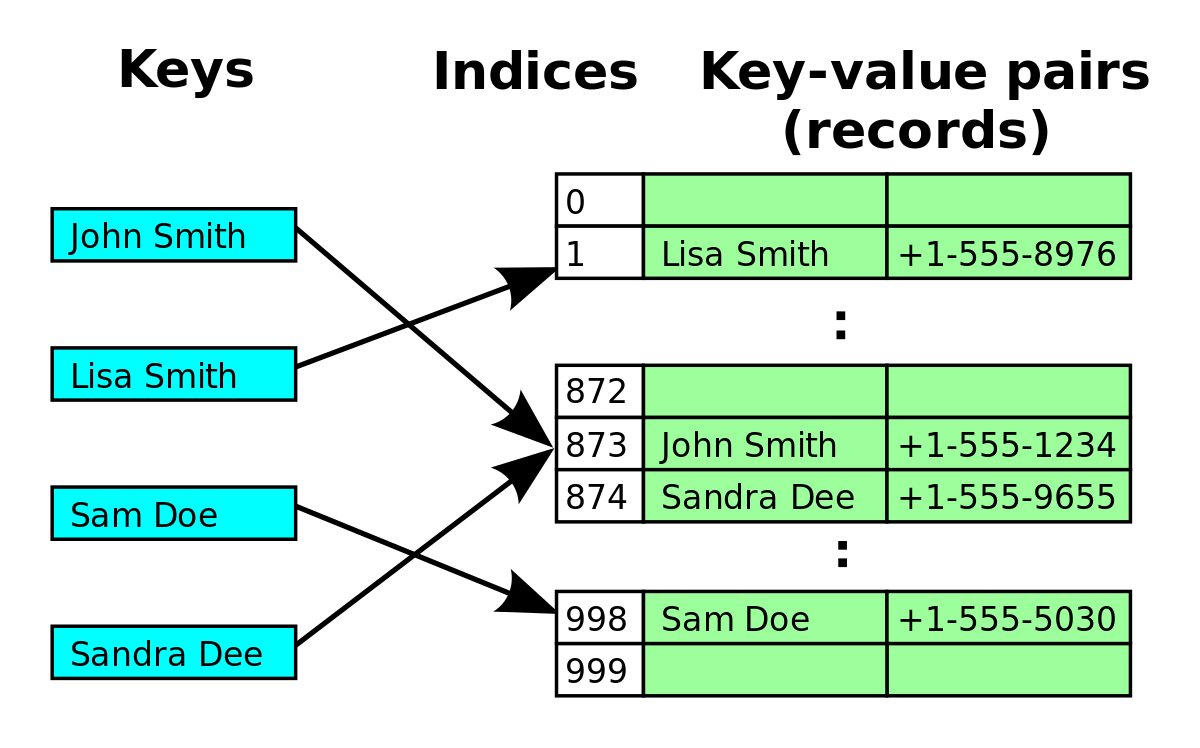
● 해싱: key에 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 직접 접근하는 탐색
- 해시 테이블: 키에 대한 연산에 의해 직접 접근이 가능한 구조
- 컴바일러가 사용하는 심볼 테이블, 철자 검사기, 데이터베이스 등에서 활용
- O(1)의 시간안에 탐색을 마칠 수 있음
14.2 추상 자료형 사전
● 사전: (키, 값)의 쌍으로, 키와 관련된 값을 동시에 저장하는 자료구조. map이나 table로도 불림
키(key): 사전의 단어처럼 항목과 항목을 구별시켜주는 것
값(value): 단어의 설명에 해당
- 항목들의 위치는 상관없으며 키만 알고 있으면 항목에 접근하고 삭제할 수 있다.
- 리스트는 위치에 의해 관리되는 자료구조인 반면, 사전은 오직 키에 의해서만 관리됨
● 사전의 연산
add(key,value): (key,value)를 사전에 추가
delete(key): key에 해당하는 값을 찾아서 삭제, 해당 value를 return. 탐색 실패 시 NULL을 return
search(key): key에 해당하는 값을 찾아서 return, 탐색 실패 시 NULL을 return
14.3 해싱의 구조
현실적으로 탐색 키들이 문자열이거나 매우 큰 숫자일 경우 탐색 키를 직접 배열의 인덱스로 사용하기 어렵다
따라서 각 탐색키를 작은 정수로 mapping시키는 함수가 필요하다.
해싱(hashig) = key만으로 바로 value가 들어있는 배열의 인덱스를 결정하는 기법
● 해시함수: 키를 입력받아 해시 주소(hash address)를 생성하고, 그 주소를 해시 테이블의 인덱스로 사용하기 위한 함수
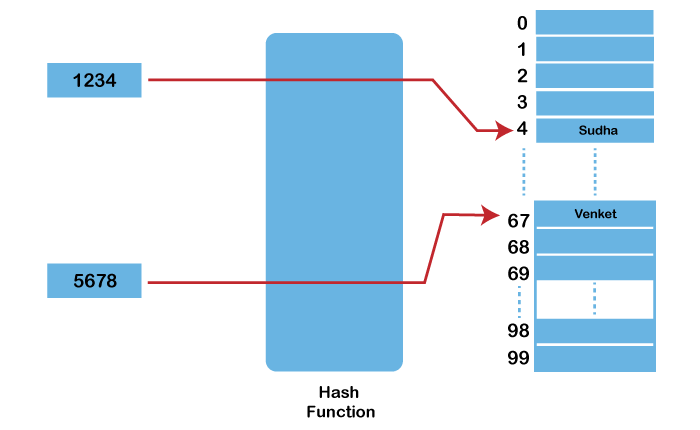
키값 k, 해시함수 h(x) -> h(k)라는 해시주소를 인덱스로 하여 해시 테이블에 접근
- 해시테이블 ht는 M개의 버킷으로 이루어짐.
-> 0 ≤ h(k) ≤ M-1
- 하나의 버킷은 s개의 슬롯을 가질 수 있으며 하나의 슬롯에는 하나의 항목이 저장됨 (위 그림에선 s=1)
● 충돌: 버킷 수 M은 보통 모든 키의 경우의 수보다 매우 작으므로 서로 다른 키가 해시함수에 의해
같은 해시 주소로 mapping되는 경우. 이 때 키 k1와 k2는 동의어(synonym)
- 충돌 발생 시 같은 버킷 내 다른 슬롯에 항목을 저장.
- 슬롯의 수보다 더 많은 충돌이 발생하면 버킷에 항목을 저장할 수 없게 되는 오버플로우 발생
*슬롯의 수 s=1이면 충돌 = 바로 오버플로우
- 충돌이 잦으면 버킷 내부에서의 순차 탐색 시간이 길어져 탐색 성능 저하
-> 해시함수 개선 or 해시 테이블 크기 조정
● 이상적인 해싱
해시테이블이 충분한 공간을 가지며 슬롯의 수가 1이면 충돌이 없거나 슬롯도 충분하여 오버플로우가 발생하지 않는 경우
add(key, value):
index <- hash_func(key)
ht[index] = value
search(key):
index <- hash_func(key)
return ht[index]
● 실제의 해싱
키는 많은데 그에 비해 해시테이블의 크기는 작기에 키 하나당 공간을 할당하기 어렵다.
EX) 키를 해시테이블의 크기로 나누어 그 나머지를 해시 테이블의 주소로 하는 방식
- 0~M-1까지의 숫자가 생성되기 때문에 해시테이블에 대해 유효한 인덱스가 된다
- h(k) = k mod M
해시함수를 사용하여 효율적으로 mapping하여 충돌 및 오버플로우를 줄여야한다.
실제의 해싱에서는 충돌과 오버플로우 때문에 시간 복잡도는 이상적인 경우의 O(1)보다 떨어진다.
♠ 542p Quiz
01
| 버킷번호 | 슬롯0 | 슬롯1 |
| 0 | 100(6) | 710(10) |
| 1 | ||
| 2 | 812(8) | |
| 3 | 53(1) | 763(7) |
| 4 | 374(2) | |
| 5 | 225(3) | 65(9) |
| 6 | ||
| 7 | 557(4) | |
| 8 | 818(12) | |
| 9 | 19(5) |
123(11) 삽입 시 오버플로우 발생
∴ 충돌 횟수: 3 오버플로우: 1
14.4 해시함수
좋은 함수의 조건 3가지
- 충돌이 적어야 함
- 해시함수 값 h(k)이 해시테이블의 주소 여역 내에서 고르게 분포
- 계산이 빨라야 함
● 제산 함수: 나머지 연산자 mod를 이용하여 키를 해시 테이블의 크기로 나눈 나머지를 해시주소로 사용
h(k) = k mod M
- 함수의 값 범위는 0 ≤ h(k) ≤ M-1
- M은 주로 소수로 선택. 가령 M이 짝수면 k mod M은 k가 짝수일 때 짝수, 홀수 일 때 홀수이기 때문에
편향된 테이블 활용을 하게 된다.
- 나머지 연산 수행했을 대 음수가 나올 땐 결과값에 M을 더해서 결과값이 0 ≤ h(k) ≤ M-1에 위치하도록 한다.
int hash_func(int key){
int hash_index = key % M;
if (hash_index <0)
hash_index += M;
return hash_index;
}
● 폴딩 함수: 키의 일부를 사용하는 것이 아닌 키를 몇 개의 부분으로 나누어 이를 덧셈이나 비트별 XOR과 같은
부울 연산을 하는 등의 방법으로 주소를 구하는 함수
ex) 32비트 키를 2개의 16비트로 나누어 비트별로 XOR 연산
hash_index = (short)(key ^ (key>>16))
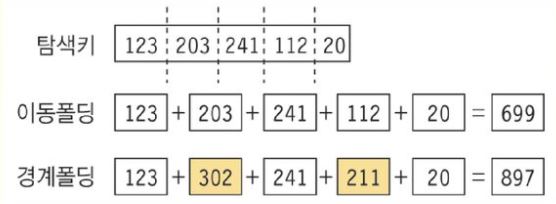
이동 폴딩: 키를 여러 부분으로 나눈 값들을 더하여 해시주소로 사용
경계 폴딩: 키의 이웃한 부분을 거꾸로 더하여 해시주소로 사용
- 주로 탐색키가 해시테이블 크기보다 더 큰 정수일 때 사용
● 중간 제곱 함수: 키를 제곱한 다음, 중간의 몇 비트를 취해서 주소 생성
- 제곱한 값의 중간 비트들은 대개 키의 모든 문자들과 관련이 있기에 서로 다른 키는 몇 개의 문자가 겹쳐도
서로 다른 해싱 주소를 가져서 고르게 분산된다.
● 비트 추출 방법: 테이블의 킉가 M=2^k 일 때 키를 이진수로 간주하여 임의의 위치의 k개의 비트를
해시 주소로 사용 , but 키의 일부 정보를 선택해서 사용하므로 편향 현상이 일어날 가능성이 높음
● 숫자 분석 방법: 숫자로 구성된 키에서 각각의 위치에 있는 수의 특징을 미리 알고 있을 때 사용
ex) 학생의 학번이 200212345이면 2002는 편향된 키이므로 나머지 수를 조합하여 해시 주소로 사용
● 탐색키가 문자열일 경우 주의할 점
- a~z를 1부터 26을 할당하거나, 아스키코드값이나 유니코드값 사용
첫번째 문자의 아스키 코드값만을 해시주소로 사용하면 -> 같은 문자로 시작하는 문자열끼리 충돌
ex) cup, car, can ..
각 문자의 아스키 코드 값을 더해서 해시주소로 사용하면 -> 동일한 문자로 이루어져있고 순서만 다른 문자열 충돌
ex) cup, puc, ucp, pcu ..
아스키 코드 값에 위치에 기초한 값을 곱하는 방법
문자열 s가 n개의 문자를 가지고 있으며 i번째 문자는 ui라고 할 때
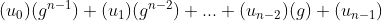
위 식을 계산량을 줄이기 위해 다음과 같은 호너의 방법(Horner's mehod)를 사용할 수 있다
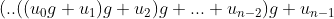
int hash_function(char *key){
int hash_index =0;
while(*key)
hash_index = g*hash_index + *key++;
return hash_index;
}
♠ 546p Quiz
01
이동폴딩: 1234 + 567 = 1801
경계폴딩: 1234 + 765 = 1999
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter14. 해싱 (2) (0) | 2024.01.20 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 13강 (0) | 2024.01.20 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter13. 탐색 (2) (2) | 2024.01.13 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter13. 탐색 (1) (1) | 2024.01.08 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 12강 (1) | 2024.01.07 |
