2.1 순환의 소개
순환(recursion): 어떤 알고리즘이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법
● 순환 호출의 내부적인 구현
- 함수가 자기 자신을 호출하는 것도 다른 함수를 호출하는 것과 동일.
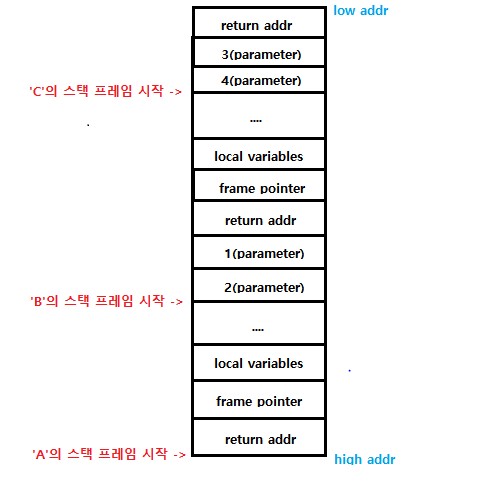
- 복귀 주소를 시스템 스택에 저장하고, 호출되는 함수를 위한 매개변수와 지역변수를 스택으로부터 할당받음.
(함수호출마다 새로운 지역변수를 만들기 때문에 이전 호출과 구분할 수 있음)
- 이 시스템 스택에서의 공간을 활성 레코드(active record)라 함.
- 호출된 함수가 끝나면, 시스템 스택에서 복귀주소를 추출하여 호출한 함수로 되돌아감.
- 순환호출이 중첩될 때마다 시스템 스택에 활성화 레코드가 쌓임.
● 순환 알고리즘의 구조
int factorial (int n){
if (n<=1) return 1; // 순환을 멈추는 부분
else return n*factorial(n-1); // 순환을 호출하는 부분
}if (n <=1)과 같이 순환 호출을 멈추는 부분이 없다면 시스템 스택을 다 사용할 때까지 순환적으로 호출되다가 오류가 발생
● 순환 ↔ 반복, 순환 알고리즘의 성능
int factorial (int n){
if (n<=1) return 1;
else return n*factorial(n-1);
}// 순환으로 팩토리얼 표현int factorial_iter(int n){
int i , result =1;
for(i=1; i<=n; i++){
result = result * i;
}
return result;
}// 반복으로 팩토리얼 표현- 반복이란 for나 while 등의 반복구조로 되풀이하는 방법이다.
- 반복과 순환은 기본적으로 문제 해결 능력이 같지만 각각 유리한 경우가 구분되며 서로 바꾸어 쓸 수가 있다.
※ 반복과 비교하였을 때 순환의 특징
- 문제의 정의가 순환적으로 되어 있는 경우에 더 유리하다. (팩토리얼, 피보나치수열, 이항계수, 이진트리 알고리즘..)
- 가독성이 더 좋고, 코딩이 쉽다.
- 여분의 기억공간이 필요하다.(호출하는 함수의 상태를 기억)
- 시간 복잡도가 같더라도 수행 시간이 더 걸린다.(매개변수들을 스택에 저장)
● 순환의 원리
- 주어진 문제를 더 작은 동일한 문제들로 분해하여 해결하는 방법인 분할정복(divide and conquer)을 사용한다.
- 해결된 부분과 남아있는 부분으로 구분되며 남아있는 부분에 대해서만 순환호출이 이루어진다.
- 순환호출이 일어날 때마다 문제의 크기는 작아진다.
♠ 50p Quiz
01 10+7+4+1+0 = 22
02
int sub(int n){
int sum =0;
for(int i=10;i>0;i--){
sum += i;
i -= 2;
}
return sum;
}
2.2 거듭제곱값 계산
순환적인 방법이 반복적인 방법보다 빠른 예시로 거듭제곱값 계산이 있다.
순환의 특성에 집중하여 ①순환을 멈추는 부분이 있는지, ②순환호출이 일어날 때마다 문제의 크기가 작아지는지
유의하면서 문제를 풀어본다.
double power(double x, int n){
if(n==0) return 1; // 순환을 멈춘다
else if ((n%2)==0)
return power(x*x, n/2);
else return x*power(x*x, (n-1)/2);
}순환호출이 이루어질 때마다 문제의 크기는 약 절반으로 줄어든다.
순환호출 횟수를 k번이라고 하면 n=2^k 이므로 양변에 로그함수를 취하면 log2n=k, 시간 복잡도는 O(log2n)이 된다.
반복적인 기법을 사용하면 n개의 루프에서 한번의 곱셈을 하므로 O(n)인 것에 비해 순환이 더 효율적이다.
♠ 53p Quiz
01 power(2,6) = power(4,3) = power(16,1)*4 = power(256,0)*16*4 = 1*16*4= 64
02 O(n), n이 -1씩 줄어들기 때문에 실행 시간이 줄어들지 않는다.
2.3 피보나치 수열의 계산
int fib(int n){
if(n==0) return 0;
if(n==1) return 1;
return (fib(n-1) + fib(n-2));
}// 순환적인 피보나치 수열 계산int fib_iter(int n){
if(n==0) return 0;
if(n==1) return 1;
int pp=0;
int p=1;
int result=0;
for(int i=2;i<=n;i++){
result = p+pp;
pp = p;
p = result;
}
}// 반복적인 피보나치 수열 계산순환적인 피보나치 수열 알고리즘은 fib(6)을 구하기 위해서도 fib(3)이 3번이나 별도로 계산되고, n이 25 정도만 돼도
거의 25만번의 호출을 하여야 해서 비효율적. O(2^n)의 시간복잡도 패턴을 가진다.
반면 반복적인 피보나치수열 알고리즘은 for문에서 O(n)의 시간복잡도를 가지기 때문에 더 효율적이다.
♠ 56p Quiz
01 fib(5) = fib(3) + fib(4) = fib(1) +fib(2) +fib(2)+fib(3) = fib(1) +fib(0) +fib(1)+ fib(0) +fib(1)+ fib(2)
02 O(b)
03 O(2^n)
2.4 하노이탑 문제
#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to)
{
if(n == 1) printf("원판 1을 %c에서 %c으로 옮긴다.\n", from, to);
else {
hanoi_tower(n - 1, from, to, tmp);
printf("원판 %d을 %c에서 %c으로 옮긴다. \n", n, from, to);
hanoi_tower(n - 1, tmp, from, to);
}
}
int main(void)
{
hanoi_tower(4, 'A', 'B', 'C');
return 0;
}else{
① from의 맨 밑의 원판을 제외한 나머지 원판들을 tmp로 옮긴다.
② from에 있는 한 개의 원판을 to로 옮긴다.
③ tmp의 원판들을 to로 옮긴다.
}
hanoi_tower함수는 from에서 tmp를 '통해서' to로 이동하는 걸 목표로 하는데,
여기서 ① step은 to를 '통해서' tmp로 이동할 것이므로 tmp 변수가 있는 두 번째 파라미터 자리에 to를 넣은 것이고
③ step은 from을 '통해서' to로 이동할 것이므로 tmp 변수가 있는 두번째 파라미터 자리에 from을 넣은 것.
♠ 62p Quiz
01 ②
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 2강 (0) | 2023.10.21 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 1강 (0) | 2023.10.21 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter3. 배열, 구조체, 포인터 (2) (0) | 2023.10.21 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter3. 배열, 구조체, 포인터 (1) (0) | 2023.10.21 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter1. 자료구조와 알고리즘 (0) | 2023.10.12 |
