3.1 배열
● 배열의 개념
배열 : 동일한 타입의 데이터를 한 번에 여러 개 만들 때 사용하는 자료형으로 대부분의 프로그래밍 언어에서
기본적으로 제공되는 자료형이다.
- 연속적인 메모리 공간이 배열에 할당되기 때문에 인덱스(index) 번호를 사용하여 쉽게 데이터에 접근이 가능하다.
● 배열 ADT
- 배열은 <인덱스, 값>의 쌍으로 이루어진 집합으로 정의할 수 있다. 즉, 인덱스에 대응하는 값(value)이 존재한다.
- 수학적으로 배열은 인덱스→값으로의 1:1 매핑(mapping)에 해당된다.
- create(size) 함수로 size개의 요소를 저장하는 배열을 생성한다.
- 주어진 인덱스에 값을 저장하는 set연산 / 인덱스로부터 대응되는 값을 추출하는 get연산이 있다.
* get함수는 배열과 인덱스를 받고, 인덱스가 유효하다면 대응되는 값을 반환하고 유효하지 않다면 오류를 반환한다.
* set함수는 배열, 인덳, 값을 받아서 새로운 인덱스 위치에 값과 함께 저장한다.
● C언어에서의 1차원 배열 , 2차원 배열
int list[6]; // create
list[0] = 100; // set
value = list[0]; //get- c에서 배열의 인덱스는 0으로 시작한다.
- 첫번째 요소인 list[0]의 주소가 배열의 기본주소가 되고, 다른 요소들은 (자료형 크기*인덱스)의 주소를 가진다.
- 위의 예시에서 list[i]의 주소는 list[0]+i*sizeof(int)이다.
int list[3][5];위의 선언에서는 3개의 행과 5개의 열을 가지는 2차원 배열이 생성된다.
- C언어에서는 배열의 배열을 만들어서 2차원 배열을 구현한다.
♣ 73p Quiz
01 get함수와 set함수로 구현되었다.
02 base+5*sizeof(int)
3.2 구조체
● 구조체의 개념
구조체 : 타입이 다른 데이터를 묶어서 하나의 객체로 사용할 수 있게 하는 자료형
struct 구조체이름{항
항목1;
항목2;
...
};
struct 구조체이름 구조체변수; // CASE1
구조체변수.항목1 = !@#$;
구조체변수.항목2 = %^&*; // CASE3
typedef struct 구조체이름{
항목1;
항목2;
...
}새로운이름;
새로운이름 구조체변수; // CASE2
새로운이름 구조체변수 = {항목1의 값, 항목2의 값, ...}; // CASE4CASE1에서는 구조체와 구조체를 구별할 수 있게 해주는 식별자인 구조체 태그를 struct와 함께 나타내야 했지만
CASE2에서는 새로 선언한 '새로운이름'으로 바로 선언할 수 있다.
CASE3에서는 .이라는 멤버연산자를 사용하여 구조체 안의 멤버에 접근했지만
CASE4에서는 선언과 동시에 구조체 안의 멤버들을 초기화했다.
♣ 75p QUIZ
01 , 02, 03
typedef struct point{
int x;
int y;
} Point;
Point p1,p2;
Point p1={1,2};
Point p2={9,8};04
double get_distance(Point p1,Point p2){
int a = p1.x-p2.x;
int b = p2.x-p2.y;
double c = sqrt((a*a)+(b*b));
return c;
}3.3 배열의 응용: 다항식
응용문제들은 머리로 먼저 생각을 한 뒤 교재의 코드를 따라 치지만, 도전문제와 QUIZ에서의 요구사항을
반영할 수 있을 만큼 코드와 구현원리에 대한 이해를 확실히 한다.
● 첫 번째 방법
10x^5+0*x^4+0*x^3+0*x^2+6x+3과 같은 다항식을 (10, 0, 0, 0, 6, 3)과 같이 모든 차수에 대한 계수값들을
리스트로 담아내 배열 coef에 저장한다. 배열 coef와 다항식의 차수를 변수 degree에 담아 같은 구조체에 저장한다.
두 다항식의 차수를 비교하여 새로운 다항식 C에 적절한 계수를 담는다.
#include <stdio.h>
#define MAX(a,b) (((a)>(b)?(a):(b)))
#define MAX_DEGREE 101
typedef struct{
int degree;
float coef[MAX_DEGREE];
} polynomial;
int start= 0; // 두 다항식의 최고차항의 계수 합이 0이 아닌 차수까지 이동시켜주는 포인터
polynomial poly_add1(polynomial A,polynomial B){
polynomial C;
int Apos=0;
int Bpos=0;
int Cpos=0;
int degree_a = A.degree;
int degree_b = B.degree;
int Apointer = A.degree; // 최고차항을 가르키는 포인터
C.degree = MAX(A.degree,B.degree);
while(Apos<=A.degree && Bpos<=B.degree){
if(degree_a>degree_b){
C.coef[Cpos++]=A.coef[Apos++];
degree_a--;
}
else if(degree_a == degree_b){ // 두 다항식 둘다
if(degree_a==Apointer){ // 최고차항이라면
if(A.coef[start]+B.coef[start]==0){ //최고차항의 계수의 합이 0인지 확인
start++; // 포인터를 옮겨준다
Apointer--;
}
}
C.coef[Cpos++]= A.coef[Apos++] + B.coef[Bpos++];
degree_a--;
degree_b--;
}
else{
C.coef[Cpos++] = B.coef[Bpos++];
degree_b--;
}
}
return C;
}
void print_poly(polynomial p){
for(int i=start;i<p.degree;i++){ // 포인터 위치부터 출력을 시작해준다
printf("%3.lfx^%d + ",p.coef[i],p.degree-i);
}
printf("%3.lf\n",p.coef[p.degree]);
}
int main(){
polynomial a= {4,{6,0,0,0,10}};
polynomial b= {4,{-6,0,5,0,1}};
polynomial c;
print_poly(a);
print_poly(b);
c= poly_add1(a,b);
printf("-------------------------------\n");
print_poly(c);
return 0;
}78p 도전문제까지 해결한 예시이다.
6x^4 + 0x^3 + 0x^2 + 0x^1 + 10
-6x^4 + 0x^3 + 5x^2 + 0x^1 + 1
-------------------------------
5x^2 + 0x^1 + 11위와 같이 다항식 C의 최고차항이 0이 아닌 차수부터 출력한다.
● 두 번째 방법
다항식의 0이 아닌 항들만 (계수, 차수)의 형식으로 구조체 배열에 저장한다.
10x^5+6x+3인 경우 ((10, 5), (6, 1), (3, 0))으로 표시한다.
구조체 배열에서 다항식 A와 다항식 B의 정보를 담은 뒤 현재 비어있는 요소의 인덱스를 가리키는 avail 변수를 설정한다.
하나의 구조체 배열에 두 다항식의 정보를 넣다 보니 각 다항식의 시작과 끝에 대한 인덱스 변수가 필요하다.
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 101
typedef struct{
float coef;
int expon;
}polynomial;
polynomial terms[MAX_TERMS] = {{8,3},{7,1},{1,0},{10,3},{3,2},{1,0}};
int avail =6;
char comp(int a, int b){
if(a>b) return '>';
else if (a ==b) return '=';
else return '<';
}
void attatch(float coef, int expon){
if(avail>MAX_TERMS){
fprintf(stderr,"항 개수 초과");
exit(1);
}
terms[avail].coef = coef;
terms[avail].expon = expon;
avail++;
}
void poly_add2(int As,int Ae,int Bs, int Be, int *Cs, int *Ce){
float tempcoef;
*Cs = avail;
while(As<=Ae && Bs<=Be){
switch(comp(terms[As].expon,terms[Bs].expon)){
case '>':
attatch(terms[As].coef,terms[As].expon);
printf(">avail call ");
As++; break;
case '=':
tempcoef = terms[As].coef + terms[Bs].coef;
if(tempcoef !=0) {
attatch(tempcoef,terms[As].expon);
printf("=avail call ");
}
As++; Bs++; break;
// 여기 break; 안걸어줬다가 두시간은 헤맸다..
case '<':
attatch(terms[Bs].coef,terms[Bs].expon);
printf("<avail call ");
Bs++; break;
}
}
for(;As<=Ae;As++){
attatch(terms[As].coef,terms[As].expon);
printf("AAavail call ");
}
for(;Bs<=Be;Bs++){
attatch(terms[Bs].coef,terms[Bs].expon);
printf("BBavail call ");
}
*Ce = avail-1;
}
void print_poly(int s, int e){
for(int i=s;i<e;i++){
printf("%3.lfx^%d + ",terms[i].coef,terms[i].expon);
}
printf("%3.lfx^%d\n",terms[e].coef,terms[e].expon);
}
int main(){
int As=0, Ae = 2, Bs = 3, Be = 5, Cs, Ce;
poly_add2(As,Ae,Bs,Be,&Cs,&Ce);
printf("%d %d %d %d %d %d\n",As,Ae,Bs,Be,Cs,Ce);
print_poly(As,Ae);
print_poly(Bs,Be);
printf("----------------------\n");
print_poly(Cs,Ce);
return 0;
} 0 2 3 5 6 10
8x^3 + 7x^1 + 1x^0
10x^3 + 3x^2 + 1x^0
----------------------
18x^3 + 3x^2 + 7x^1 + 2x^0 + 18x^3이런 식으로 마지막 Ce가 9가 아닌 10을 가리켜서 오류가 났었는데
해결방법을 못 찾다가 switch문에서 break를 제대로 안 걸어준 것을 발견했다..
=avail call <avail call >avail call =avail call 0 2 3 5 6 9
8x^3 + 7x^1 + 1x^0
10x^3 + 3x^2 + 1x^0
----------------------
18x^3 + 3x^2 + 7x^1 + 2x^0avail call이라는 디버깅용 코드를 적어서 오류를 찾아냈다.
기록용으로 남겨두겠다.
♣83p Quiz
01 polynomial a = {3, {6, 8, 0, 9}}
02 polynomial a[] = {{6, 3}, {8, 2}, {9, 0}}
03
tempcoef = terms[As].coef - terms[Bs].coef;
case '<':
attatch(-terms[Bs].coef,terms[Bs].expon);
Bs++; break;04 05 Skip
3.4 배열의 응용: 희소행렬
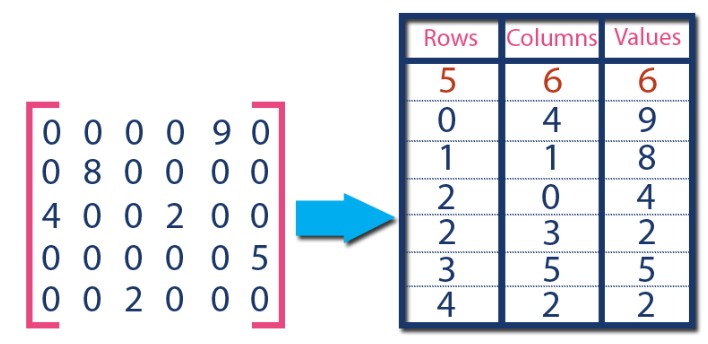
좌측 행렬처럼 많은 항들이 0으로 되어 있는 희소행렬의 경우 모든 0을 표현하면 메모라 낭비가 심하므로
우측 표처럼 (행, 열, 값)을 배열에 담는 표현이 가능하다. (전치 행렬 계산하기 #2)
● 전치 행렬 계산하기 #1
void transpose(int A[rows][cols], int B[rows][cols])
{
for(int r=0; r<rows ; r++){
for(int c=0; c<cols; c++){
B[c][r] = A[r][c]; // A의 행과 열을 바꾼 이차원 배열을 만든다
}
}
}위와 같은 방식으로 행과 열을 싹 다 바꾼 행렬을 만들 수 있다.
● 전치 행렬 계산하기 #2
구조체 element에 (행, 열, 값)을 담고, 구조체 배열 element data[MAX_TERMS]를
희소배열 구조체 SparseMatrix에 행, 열 , 항의 개수와 함께 담아서 표현한다.
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 100
typedef struct{
int row;
int col;
int value;
}element;
typedef struct{
element data[MAX_TERMS];
int rows;
int cols;
int terms;
}SparseMatrix;
SparseMatrix matrix_transpose(SparseMatrix a){
SparseMatrix b;
int bindex;
b.rows = a.rows;
b.cols = a.cols;
b.terms = a.terms;
if(a.terms>0){
bindex=0;
for(int n=0;n<a.cols;n++){ // 기존 행렬의 열이 행으로 바뀌니까 열기준
for(int i=0; i<a.terms; i++){ // 0이 아닌 항의 개수만큼
if(a.data[i].col == n){
// 열기준으로 같은 값이 있으면 새 행렬에 넣자
b.data[bindex].row= a.data[i].col;
b.data[bindex].col= a.data[i].row;
b.data[bindex].value= a.data[i].value;
bindex++;
}
}
}
}
return b;
}
void matrix_print(SparseMatrix a){
printf("================\n");
for(int i=0; i<a.terms;i++){
printf("%d %d %d\n",a.data[i].row, a.data[i].col,a.data[i].value);
}
printf("================\n");
}
int main(){
SparseMatrix m = {
{{0,3,7},{1,0,9},{1,5,8},{3,0,6},{3,1,5},{4,5,1},{5,2,2}},
6,
6,
7
};
SparseMatrix result;
result = matrix_transpose(m);
matrix_print(result);
}
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 2강 (0) | 2023.10.21 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 1강 (0) | 2023.10.21 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter3. 배열, 구조체, 포인터 (2) (0) | 2023.10.21 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter2. 순환 (0) | 2023.10.14 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter1. 자료구조와 알고리즘 (0) | 2023.10.12 |
