8.1 트리의 개념
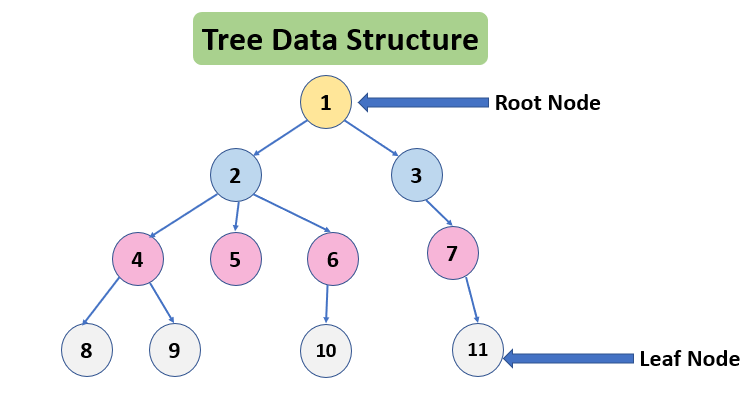
트리: 계층적인 자료구조로, 가족의 가계도, 회사의 조직도, 인공지능의 결정 트리 등에 사용된다.
● 트리의 용어들
노드: 트리의 구성 요소에 해당하는 각각의 데이터셋
루트 노드: 계층구조에서 최상단에 위치하는 노드
서브 노드: 루트 노드를 제외한 나머지 노드
간선(edge): 루트와 서브트리를 연결하는 선
서브트리: 특정 노드에 대한 하위 노드들의 집합
부모 노드 , 자식노드, 형제노드: 가계도에서의 위치 및 관계와 유사한 노드
조상 노드: 루트 노드~ 임의의 노드까지의 경로를 이루고 있는 노드들
후손 노드: 임의의 노드 하위에 연결된 모든 노드들(특정 노드의 서브트리에 속하는 모든 노드)
단말 노드: 자식 노드가 없는 노드/ terminal node 또는 leaf node / 반대는 비단말 노드
노드의 차수: 어떤 노드가 가지고 있는 자식 노드의 개수 / 단말 노드의 차수는 0
트리의 차수: 트리가 가지고 있는 노드의 차수 중에서 가장 큰 값
트리의 레벨: 트리의 각층에 번호를 매긴 것으로, 루트의 레벨은 1
트리의 높이: 트리가 가지고 있는 최대 레벨
포리스트(forest): 트리들의 집합
● 트리의 종류
- 각 노드는 데이터를 저장하는 데이터필드에 자식 노드의 개수만큼 자식 노드를 가리키는 링크 필드를 가진다.
♠ 257p Quiz
01 단말노드
02 차수
03 50, 33, 14, 2, 3
8.2 이진 트리 소개
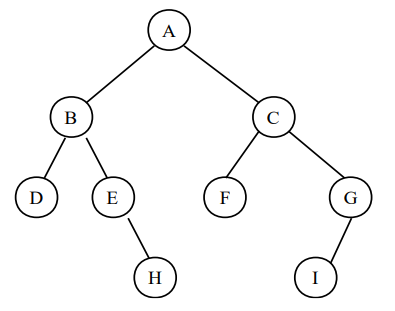
이진 트리: 모든 노드가 2개의 서브 트리를 가지고 있는 트리로,
공집합이거나 / 루트, 왼쪽 서브 트리, 오른쪽 서브 트리로 구성된 노드들의 유한 집합.
- 이진 트리의 서브 트리들은 모두 이진트리
- 서브 트리는 공집합일 수 있다.
- 따라서 각 노드는 최대 2개까지의 자식 노드를 가질 수 있으며 모든 노드의 차수는 2 이하이다.
- 서브 트리 사이에는 순서가 존재하며 따라서 왼쪽 서브트리와 오른쪽 서브트리는 서로 구분된다.
- 이진 트리는 노드를 하나도 갖지 않을 수도 있다.
● 이진트리의 성질
- 노드의 개수가 n이면 이진트리는 n-1개의 간선을 가진다.(루트를 제외하기 때문)
- 높이가 h면 이진트리는 최소 h개, 최대 2^h-1개의 노드를 가진다.
(레벨이 1이면 루트노드만 가지고 나머지 레벨에선 최대 2개의 노드를 가지기 때문)
- 노드의 개수가 n이면 이진트리의 높이는 최대 n, 최소 ⌈log2(n+1)⌉이다.
(n≤ 2^h-1 , 양변에 log 취하여 정리하면 h≥ log2(n+1)이기 때문)
● 이진트리의 분류
- 포화 이진 트리(full binary tree) : 각 레벨에 노드가 꽉 차있는 이진트리, 높이가 k면 총 2^k-1개의 노드를 가진다.
루트 노드부터 레벨 단위로 왼쪽에서 오른쪽으로 내려오면서 번호를 붙인다.
ex) 루트노드의 오른쪽 자식 노드의 번호는 항상 3
- 완전 이진 트리(complete binary tree) : 높이가 k일 때 레벨 1~k-1까지는 노드가 모두 채워져 있고,
마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리.
* 포화 이진트리는 항상 완전 이진 트리지만 그 역은 성립하지 않는다.
* 포화 이진트리의 노드 번호들과 1대1로 대응한다.
♠ 263p Quiz
01 e = n-1
02 2^h -1
03 최대 n, 최소 ⌈log2(n+1)⌉
8.3 이진 트리의 표현
● 배열 표현법
- 포화 이진 트리나 완전 이진 트리에서 자주 사용
- 이진 트리의 높이가 k일 때 2^k-1 개의 공간을 연속적으로 할당한 다음, 완전 이진트리의 번호 부여
- 노드 번호가 1부터 시작하기 때문에 인덱스0 또한 사용하지 않는다.
- 기억 공간의 낭비가 심함
- 인덱스만 알면 노드의 부모나 자식을 바로 알 수 있으며 다음과 같은 공식이 성립
[ 노드 i의 부모 노드 인덱스 = i/2, 노드 i의 왼쪽 자식 노드 인덱스 = 2i, 노드 i의 오른쪽 자식 노드 인덱스 = 2i+1]
● 링크 표현법
- 각 노드는 2개의 포인터를 가진 구조체로 표현, 각 포인터는 왼쪽 자식노드와 오른쪽 자식노드를 가리킨다.
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
} TreeNode;
- 노드들을 동적 할당을 통해 생성하면 트리의 확장이 가능하다.
int main(){
TreeNode *n1, *n2 *n3;
n1 = (TreeNode*)malloc(sizeof(TreeNode));
n2 = (TreeNode*)malloc(sizeof(TreeNode));
n3 = (TreeNode*)malloc(sizeof(TreeNode));
n1->data =10;
n1->left = n2;
n1->right = n3;
.
.
.
♠ 266p Quiz
01 10:1 20:3 30:7 25:14
02 skip
8.4 이진 트리의 순회
이진 트리를 순회(traversal): 이진트리에 속하는 모든 노드를 한 번씩 방문하는 것
- 스택이나 큐와 같은 선형 자료구조와 달리 여러 순서로 노드에 접근할 수 있다.
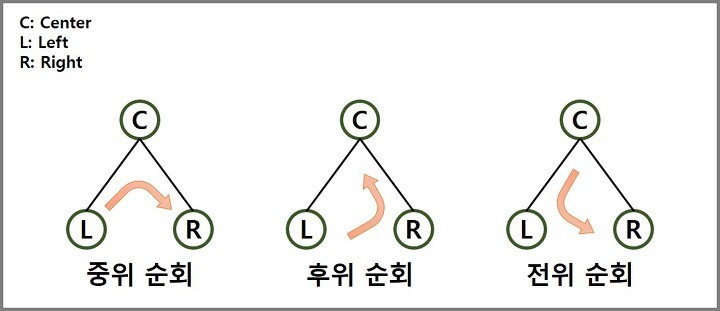
루트 방문 = V, 왼쪽 서브트리 방문 = L, 오른쪽 서브트리 방문 = R이라고 하면
전위순회: VLR 중위순회: LVR 후위순회: LRV
항상 왼쪽 서브트리를 오른쪽 서브트리에 앞서서 방문한다.
순환적 순회: 서브트리를 순회하는 것은 전체 트리를 순회하는 것과 유사하기에 루트노드만 바꾸어 함수를 호출하는 방법
- 서브트리와 전체 트리의 구조는 같고, 문제의 크기만 줄어들기 때문에 순환을 적용할 수 있다.
- 전체 트리의 루트노드를 매개변수로 한 함수 안에서 서브트리를 방문할 때는
서브트리의 루트 노드 포인터를 함수의 매개변수로 사용한다.
void inorder(TreeNode *root){
if(root !=NULL){
inorder(root->left);
printf("[%d] ",root->data);
inorder(root->right);
}
}
void preorder(TreeNode *root){
if(root !=NULL){
printf("[%d] ",root->data);
preorder(root->left);
preorder(root->right);
}
}
void postorder(TreeNode *root){
if(root !=NULL){
postorder(root->left);
postorder(root->right);
printf("[%d] ",root->data);
}
}
편의를 위해 노드를 정적으로 만들어 전역 변수로 정의한 예제
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
}TreeNode;
TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, &n1, NULL};
TreeNode n3 = {16, NULL, NULL};
TreeNode n4 = {25, NULL, NULL};
TreeNode n5 = {20, &n3, &n4};
TreeNode n6 = {15, &n2, &n5};
TreeNode *root = &n6;
void inorder(TreeNode *root){
if(root !=NULL){
inorder(root->left);
printf("[%d] ",root->data);
inorder(root->right);
}
}
void preorder(TreeNode *root){
if(root !=NULL){
printf("[%d] ",root->data);
preorder(root->left);
preorder(root->right);
}
}
void postorder(TreeNode *root){
if(root !=NULL){
postorder(root->left);
postorder(root->right);
printf("[%d] ",root->data);
}
}
int main(){
printf("중위 순회=");
inorder(root);
printf("\n");
printf("전위 순회=");
preorder(root);
printf("\n");
printf("후위 순회=");
postorder(root);
printf("\n");
}
8.5 반복적 순회
반복적 순회: 별도의 스택에 자식 노드들을 저장하고 꺼내면서 순회하는 방법
교재와 달리 전위 순회를 구현해 보았다.
전위 순회 결과 =[15] [4] [1] [20] [16] [25]
전위 순회는 루트노드, 왼쪽 서브트리 노드, 오른쪽 서브트리 노드 순으로 방문해야 하므로
스택에 push 할 때는 오른쪽 서브트리 노드를 먼저 push 하고 그 후 왼쪽 서브트리 노드를 push 한다.
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
#define SIZE 100
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
}TreeNode;
int top = -1;
TreeNode *stack[SIZE];
void push(TreeNode *p){
if(top<SIZE-1){
stack[++top] = p;
}
}
TreeNode *pop(){
TreeNode *p = NULL;
if(top >= 0){
p = stack[top--];
}
return p;
}
void preorder_iter(TreeNode *root){
push(root);
while(top>=0){
TreeNode *stacktop = stack[top];
TreeNode *temp = pop();
printf("[%d] ",temp->data);
temp = stacktop->right;
if(temp != NULL){
push(temp);
}
temp = stacktop->left;
if(temp != NULL){
push(temp);
}
}
}
TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, &n1, NULL};
TreeNode n3 = {16, NULL, NULL};
TreeNode n4 = {25, NULL, NULL};
TreeNode n5 = {20, &n3, &n4};
TreeNode n6 = {15, &n2, &n5};
TreeNode *root = &n6;
int main(){
printf("전위 순회=");
preorder_iter(root);
printf("\n");
}
8.6 레벨 순회
레벨 순회: 레벨 1인 루트 노드부터 레벨 순으로 각 노드를 검사하는 순회 방법
- 앞선 순회들과 달리 스택이 아닌 큐를 사용한다.
- 큐를 dequeue() 하여 꺼낸 노드의 자식 노드를 큐에 enqueue() 하는 것을 반복한다.
- 포화 이진 트리에 할당한 번호에 대응되는 순서로 노드를 enqueue 하기에 왼쪽 서브트리 노드부터 삽입한다.
void level_order(TreeNode *ptr){
QueueType q;
init_queue(&q);
if(ptr == NULL) return;
enqueue(&q,ptr);
while(!is_empty(&q)){
ptr = dequeue(&q);
printf("[%d] ",ptr->data);
if(ptr->left){
enqueue(&q,ptr->left);
}
if(ptr->right){
enqueue(&q,ptr->right);
}
}
}
● 어떤 순회를 선택하여야 할까?
- 순서가 중요하지 않다면 어떤 순회를 사용하여도 무방하다.
- 자식 노드를 처리한 다음 부모 노드를 처리해야 한다면(ex.디렉토리 용량 계산) 후위 순회를,
부모 노드를 처리한 다음 자식 노드를 처리해야 한다면 전위 순회를 사용하여야 한다.
♠ 283p Quiz
01 1
/ \
2 3
/ \
4 5
8.7 트리의 응용: 수식 트리 처리

수식 트리의 루트 노드: 연산자 각 서브트리의 자식 노드: 피연산자
피연산자인 자식 노드를 먼저 방문해야 하므로 후위 순회를 사용한다.
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
}TreeNode;
TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, NULL, NULL};
TreeNode n3 = {'*', &n1, &n2};
TreeNode n4 = {16, NULL, NULL};
TreeNode n5 = {25, NULL, NULL};
TreeNode n6 = {'+', &n4, &n5};
TreeNode n7 = {'+', &n3, &n6};
TreeNode *exp = &n7;
int evaluate(TreeNode *root){
if(root==NULL) return 0;
if(root->left == NULL && root->right ==NULL){
return root->data;
}
else{
int op1 = evaluate(root->left);
int op2 = evaluate(root->right);
printf("%d %c %d을 계산합니다.\n", op1, root->data, op2);
switch(root->data){
case '+':
return op1+op2;
case '-':
return op1-op2;
case '*':
return op1*op2;
case '/':
return op1/op2;
}
}
return 0;
}
int main(){
printf("수식의 값은 %d입니다.\n",evaluate(exp));
return 0;
}'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 8강 (2) | 2023.11.30 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] Chapter8. 트리 (2) (1) | 2023.11.28 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 7강 (1) | 2023.11.23 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter7. 연결 리스트 II (2) (0) | 2023.11.22 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter7. 연결 리스트 II (1) (1) | 2023.11.22 |
