8.9 이진 트리의 추가 연산
● 노드의 개수
- 트리안의 노드들을 전체적으로 순회하여 카운트를 센다.
int get_node_count(TreeNode *node){
int count =0;
if(node!=NULL){
count = 1+get_node_count(node->left)
+ get_node_count(node->right);
}
return count;
}
● 단말 노드 개수 구하기
- 단말 노드는 노드의 자식 노드가 없을 때만 count를 올려준다.
int get_leaf_count(TreeNode *node){
int count =0;
if(node!=NULL){
if(node->left ==NULL && node->right ==NULL){
return 1;
}
else{
count =get_leaf_count(node->left) + get_leaf_count(node->right);
}
}
return count;
}
● 높이 구하기
- 순환이 끝나면 각 서브 트리로부터 서브 트리 높이가 반환되었을 것이다.
- 반환된 서브 트리 높이 중에서 크기가 큰 값을 반환하여 순환한다.
int max(int a, int b)
{
return a < b ? b : a;
}
int get_height(TreeNode *node){
int height = 0;
if(node!=NULL){
height = 1+ max(get_height(node->left),get_height(node->right));
}
return height;
}
♠ 290p Quiz
01 상단 코드 구현
02 get_node_count()에서 get_leaf_count()를 뺀 값을 반환한다.
03 추후 구현
8.10 스레드 이진 트리
2n개의 링크들 중 n+1개의 링크는 NULL을 가리킨다. 이 NULL 링크들을 잘 사용하면
순환호출 없이 트리의 노드들을 순회할 수 있다.

● 스레드 이진 트리: 중위 순회 시에 선행 노드인 중위 선행자 혹은 후속 노드인 중위 후속자를
NULL 링크에 저장시켜 놓은 트리, 실을 이용하여 노드들은 순회 순서대로 연결된다.
- NULL링크에 스레드가 저장될 수 있다.
- 각 노드는 자식을 가리키는 포인터가 저장돼 있는지 아니면 NULL대신 스레드가 저장돼 있는지를
구별해 주는 태그 필드가 필요하다.
- 태그 필드인 is_thread가 TRUE이면 right는 중위 후속자라고 가정하고 FALSE이면
오른쪽 자식을 가리키는 포인터가 된다.
- 순회는 빠르지만 스레드를 설정하기 위해 삽입이나 삭제 시에 더 많은 일을 하여야 한다.
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
*위의 그림에서 1-3-5-6-7-8-9-11-13 순으로 중위 순회를 할 텐데, thread인 1,5, 7, 9는
right가 NULL이 아닌 중위 후속자인 오른쪽 자식을 가리킨다.
is_thread가 TRUE이면 스레드인 right를 타고 들어가 중위 후속자에 접근하고,
아니라면 오른쪽 서브트리로 이동할 텐데 그 서브트리의 가장 왼쪽 노드로 이동하도록
while(q->left != NULL) q = q->left; 를 사용한다.
TreeNode * find_successor(TreeNode *p){
TreeNode *q = p->right;
if(q == NULL || p->is_thread == TRUE){
return q;
}
while(q->left !=NULL) q = q->left;
return q;
}
전체 프로그램은 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
TreeNode n1 = {'A', NULL, NULL, 1};
TreeNode n2 = {'B', NULL, NULL,1};
TreeNode n3 = {'C', &n1, &n2, 0};
TreeNode n4 = {'D', NULL, NULL,1};
TreeNode n5 = {'E', NULL, NULL,0};
TreeNode n6 = {'F', &n4, &n5, 0};
TreeNode n7 = {'G', &n3, &n6, 0};
TreeNode *exp = &n7;
TreeNode * find_successor(TreeNode *p){
TreeNode *q = p->right;
if(q == NULL || p->is_thread == TRUE){
return q;
}
while(q->left !=NULL) q = q->left;
return q;
}
void thread_inorder(TreeNode *t){
TreeNode *q;
q=t;
while(q->left) q= q->left; //가장 왼쪽 노드로 이동
do{
printf("%c -> ",q->data);
q = find_successor(q);
}while(q);
}
int main(){
n1.right = &n3;
n2.right = &n7;
n4.right = &n6; // thread 설정
thread_inorder(exp);
printf("\n");
return 0;
}
♠ 293p Quiz
01 n+1개
02 중위 순회 시 후속 노드인 중위 후속자가 저장된다.
8.11 이진 탐색 트리
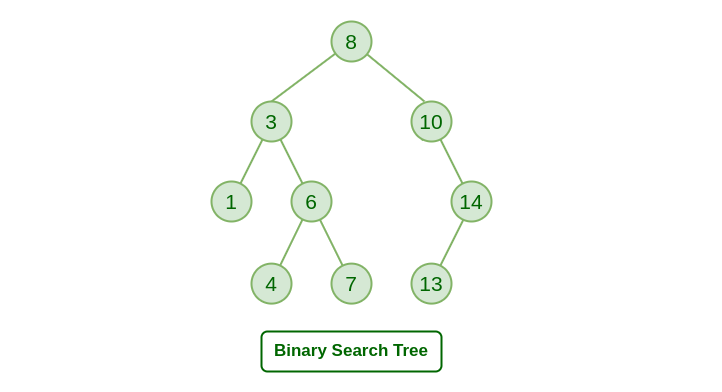
● 이진 탐색 트리(binary search tree): 이진 트리 기반의 탐색을 위한 자료구조
탐색: 레코드의 집합(테이블)에서 특정한 레코드를 찾아내는 작업
- 레코드는 하나 이상의 필드(이름, 주소, 식별번호 등)를 포함할 수 있다.
- 레코드들은 보통 key라고 불리는 하나의 필드에 의해 식별될 수 있다.
- 레코드를 식별하게 해주는, 다른 키와 중복되지 않는 고유한 값을 가지는 키를 주요키(primary key)라 한다.
※이진 탐색 트리 정의
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들을 루트 키보다 작다.
- 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
● 순환적인 탐색연산
주어진 탐색키 값과 루트 노드의 키 값을 비교
1. 비교한 결과가 같으면 탐색 종료
2. 주어진 키 값이 루트 노드의 키값보다 작으면 루트노드의 왼쪽 자식을 기준으로 재탐색
3. 주어진 키 값이 루트 노드의 키값보다 크면 루트노드의 오른쪽 자식을 기준으로 재탐색
TreeNode *search(TreeNode * node, int key){
if(node ==NULL) return NULL;
if(key == node->key) return node;
else if(key < node->key){
return search(node->left,key);
}
else{
return search(node->right,key);
}
}
● 반복적인 탐색연산
주어진 탐색키 값과 루트 노드의 키 값을 비교
1. 비교한 결과가 같으면 탐색 종료
2. 주어진 키 값이 현재 노드 키 값보다 작으면 node변수를 node->left로 변경
3. 주어진 키 값이 현재 노드 키 값보다 크면 node 변수를 node->right로 변경
4. while문 반복이 종료되었는데도 아직 함수가 return 되지 않았다면 key == node->key의 if문에
걸리지 않은 것, 즉 탐색이 실패한 것이므로 NULL을 반환한다.
*반복적인 탐색연산이 순환적인 탐색연산보다 효율성 측면에서 우수하다.
TreeNode *search_itr(TreeNode *node, int key){
while(node != NULL){
if(key==node->key) return node;
else if(key<node->key){
node = node->left;
}
else{
node = node->right;
}
}
return NULL;
}
● 이진탐색트리에서 삽입연산
삽입연산 이전에 탐색 연산을 수행하여야 한다.
1. 같은 키값을 갖는 노드가 없어야 하고
2. 탐색에서 실패한 지점이 이후 우리가 삽입연산을 수행할 위치가 되기 때문
삽입연산은 항상 단말노드에서 수행된다. 새로운 노드는 단말 노드의 하위 노드로 추가된다.
TreeNode *new_node(int item){
TreeNode *temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
TreeNode *insert_node(TreeNode *node, int key){
if(node == NULL) return new_node(key);
if(key <node->key){
node->left = insert_node(node->left,key);
}
else if(key > node->key){
node->right = insert_node(node->right,key);
}
return node;
}
● 이진탐색트리에서 삭제연산
삭제하려는 노드가 트리의 어디에 위치하는 지를 알기 위해 탐색연산부터 수행한다.
다음과 같은 3가지 경우를 고려한다.
CASE1: 삭제하려는 노드가 단말 노드
CASE2: 삭제하려는 노드가 왼쪽 또는 오른쪽 서브 트리 중 하나만 가지고 있는 경우
CASE3: 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
●CASE1: 삭제하려는 노드가 단말 노드
- 부모노드를 찾아서 부모노드 안의 링크필드를 NULL로 만들어 연결을 끊는다.
●CASE2: 삭제하려는 노드가 왼쪽 또는 오른쪽 서브 트리 중 하나만 가지고 있는 경우
- 자식 노드를 부모 노드에 붙여주고 삭제하려는 자기 노드는 삭제한다.
●CASE3: 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
- 왼쪽 서브트리의 가장 오른쪽에 있는 노드 또는 오른쪽 서브트리의 가장 왼쪽에 있는 노드를 찾아서
부모 노드에 붙여주고 삭제하려는 자기 노드는 삭제한다.
TreeNode * min_value_node(TreeNode *node){
TreeNode *current = node;
while(current->left !=NULL){
current = current->left;
}
return current;
} // 파란글씨, 오른쪽 트리의 가장 왼쪽 노드를 찾기 위함
전체 코드는 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
typedef int element;
typedef struct TreeNode{
element key;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
TreeNode *search(TreeNode * node, int key){
if(node ==NULL) return NULL;
if(key == node->key) return node;
else if(key < node->key){
return search(node->left,key);
}
else{
return search(node->right,key);
}
}
TreeNode *search_itr(TreeNode *node, int key){
while(node != NULL){
if(key==node->key) return node;
else if(key<node->key){
node = node->left;
}
else{
node = node->right;
}
}
return NULL;
}
TreeNode *new_node(int item){
TreeNode *temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
TreeNode *insert_node(TreeNode *node, int key){
if(node == NULL) return new_node(key);
if(key <node->key){
node->left = insert_node(node->left,key);
}
else if(key > node->key){
node->right = insert_node(node->right,key);
}
return node;
}
TreeNode * min_value_node(TreeNode *node){
TreeNode *current = node;
while(current->left !=NULL){
current = current->left;
}
return current;
}
TreeNode *delete_node(TreeNode *root, int key){
if(root ==NULL) return root;
if(key< root->key){
root->left = delete_node(root->left,key);
}
else if (key>root->key){
root->right = delete_node(root->right,key);
}
else{
if(root->left ==NULL){ // CASE1 or CASE2
TreeNode * temp = root->right;
free(root);
return temp;
}
else if(root->right ==NULL){
TreeNode *temp = root->left;
free(root);
return temp;
}
//CASE3
TreeNode *temp = min_value_node(root->right);
root->key = temp ->key;
root->right = delete_node(root->right,temp->key);
}
return root;
}
void inorder(TreeNode *root){
if(root){
inorder(root->left);
printf("[%d] ",root->key);
inorder(root->right);
}
}
int main(){
TreeNode * root = NULL;
TreeNode *temp = NULL;
root = insert_node(root,30);
root = insert_node(root,20);
root = insert_node(root,10);
root = insert_node(root,40);
root = insert_node(root,50);
root = insert_node(root,60);
printf("이진 탐색 트리 중위 순회 결과 \n");
inorder(root);
printf("\n");
if(search(root,30)!=NULL){
printf("트리에 30이 있음\n");
}
else{
printf("트리에 30이 없음\n");
}
return 0;
}
● 이진탐색트리의 분석
탐색, 삽입 삭제 연산의 평균적인 시간 복잡도: 트리의 높이가 h일 때 O(h),
n개의 노드를 가지는 이진 탐색 트리의 경우 일반적인 트리의 높이가 ⌈log2(n)⌉ 이므로 O(log2n)
최악의 경우: 한쪽으로 치우친 경사 트리가 되면 트리의 높이는 n이기 때문에 O(n)이 되어
선형 탐색과 같은 시간 복잡도를 가진다.
따라서 트리의 높이를 ⌈log2(n)⌉로 만들기 위해 트리를 균형지게 만드는 다양한 기법들이 있다.
균형 트리는 12장에서 다룬다.
♠ 310p Quiz
01 ⌈log2(9)⌉ = 4
02 17 14 01 26 66 28 34 80
03 26
/ \
14 28
/ \
02 66
/ \
34 80
8.12 이진 탐색 트리의 응용: 영어 사전
기존 이진 탐색 트리 코드에서 구조체를 키로 사용하는 것 외에 큰 차이점이 없어서 생략
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter9. 우선순위 큐 (1) (0) | 2023.12.01 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 8강 (2) | 2023.11.30 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter8. 트리 (1) (2) | 2023.11.25 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 7강 (1) | 2023.11.23 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter7. 연결 리스트 II (2) (0) | 2023.11.22 |
8.9 이진 트리의 추가 연산
● 노드의 개수
- 트리안의 노드들을 전체적으로 순회하여 카운트를 센다.
int get_node_count(TreeNode *node){
int count =0;
if(node!=NULL){
count = 1+get_node_count(node->left)
+ get_node_count(node->right);
}
return count;
}
● 단말 노드 개수 구하기
- 단말 노드는 노드의 자식 노드가 없을 때만 count를 올려준다.
int get_leaf_count(TreeNode *node){
int count =0;
if(node!=NULL){
if(node->left ==NULL && node->right ==NULL){
return 1;
}
else{
count =get_leaf_count(node->left) + get_leaf_count(node->right);
}
}
return count;
}
● 높이 구하기
- 순환이 끝나면 각 서브 트리로부터 서브 트리 높이가 반환되었을 것이다.
- 반환된 서브 트리 높이 중에서 크기가 큰 값을 반환하여 순환한다.
int max(int a, int b)
{
return a < b ? b : a;
}
int get_height(TreeNode *node){
int height = 0;
if(node!=NULL){
height = 1+ max(get_height(node->left),get_height(node->right));
}
return height;
}
♠ 290p Quiz
01 상단 코드 구현
02 get_node_count()에서 get_leaf_count()를 뺀 값을 반환한다.
03 추후 구현
8.10 스레드 이진 트리
2n개의 링크들 중 n+1개의 링크는 NULL을 가리킨다. 이 NULL 링크들을 잘 사용하면
순환호출 없이 트리의 노드들을 순회할 수 있다.

● 스레드 이진 트리: 중위 순회 시에 선행 노드인 중위 선행자 혹은 후속 노드인 중위 후속자를
NULL 링크에 저장시켜 놓은 트리, 실을 이용하여 노드들은 순회 순서대로 연결된다.
- NULL링크에 스레드가 저장될 수 있다.
- 각 노드는 자식을 가리키는 포인터가 저장돼 있는지 아니면 NULL대신 스레드가 저장돼 있는지를
구별해 주는 태그 필드가 필요하다.
- 태그 필드인 is_thread가 TRUE이면 right는 중위 후속자라고 가정하고 FALSE이면
오른쪽 자식을 가리키는 포인터가 된다.
- 순회는 빠르지만 스레드를 설정하기 위해 삽입이나 삭제 시에 더 많은 일을 하여야 한다.
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
*위의 그림에서 1-3-5-6-7-8-9-11-13 순으로 중위 순회를 할 텐데, thread인 1,5, 7, 9는
right가 NULL이 아닌 중위 후속자인 오른쪽 자식을 가리킨다.
is_thread가 TRUE이면 스레드인 right를 타고 들어가 중위 후속자에 접근하고,
아니라면 오른쪽 서브트리로 이동할 텐데 그 서브트리의 가장 왼쪽 노드로 이동하도록
while(q->left != NULL) q = q->left; 를 사용한다.
TreeNode * find_successor(TreeNode *p){
TreeNode *q = p->right;
if(q == NULL || p->is_thread == TRUE){
return q;
}
while(q->left !=NULL) q = q->left;
return q;
}
전체 프로그램은 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
typedef struct TreeNode{
int data;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
TreeNode n1 = {'A', NULL, NULL, 1};
TreeNode n2 = {'B', NULL, NULL,1};
TreeNode n3 = {'C', &n1, &n2, 0};
TreeNode n4 = {'D', NULL, NULL,1};
TreeNode n5 = {'E', NULL, NULL,0};
TreeNode n6 = {'F', &n4, &n5, 0};
TreeNode n7 = {'G', &n3, &n6, 0};
TreeNode *exp = &n7;
TreeNode * find_successor(TreeNode *p){
TreeNode *q = p->right;
if(q == NULL || p->is_thread == TRUE){
return q;
}
while(q->left !=NULL) q = q->left;
return q;
}
void thread_inorder(TreeNode *t){
TreeNode *q;
q=t;
while(q->left) q= q->left; //가장 왼쪽 노드로 이동
do{
printf("%c -> ",q->data);
q = find_successor(q);
}while(q);
}
int main(){
n1.right = &n3;
n2.right = &n7;
n4.right = &n6; // thread 설정
thread_inorder(exp);
printf("\n");
return 0;
}
♠ 293p Quiz
01 n+1개
02 중위 순회 시 후속 노드인 중위 후속자가 저장된다.
8.11 이진 탐색 트리

● 이진 탐색 트리(binary search tree): 이진 트리 기반의 탐색을 위한 자료구조
탐색: 레코드의 집합(테이블)에서 특정한 레코드를 찾아내는 작업
- 레코드는 하나 이상의 필드(이름, 주소, 식별번호 등)를 포함할 수 있다.
- 레코드들은 보통 key라고 불리는 하나의 필드에 의해 식별될 수 있다.
- 레코드를 식별하게 해주는, 다른 키와 중복되지 않는 고유한 값을 가지는 키를 주요키(primary key)라 한다.
※이진 탐색 트리 정의
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들을 루트 키보다 작다.
- 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
● 순환적인 탐색연산
주어진 탐색키 값과 루트 노드의 키 값을 비교
1. 비교한 결과가 같으면 탐색 종료
2. 주어진 키 값이 루트 노드의 키값보다 작으면 루트노드의 왼쪽 자식을 기준으로 재탐색
3. 주어진 키 값이 루트 노드의 키값보다 크면 루트노드의 오른쪽 자식을 기준으로 재탐색
TreeNode *search(TreeNode * node, int key){
if(node ==NULL) return NULL;
if(key == node->key) return node;
else if(key < node->key){
return search(node->left,key);
}
else{
return search(node->right,key);
}
}
● 반복적인 탐색연산
주어진 탐색키 값과 루트 노드의 키 값을 비교
1. 비교한 결과가 같으면 탐색 종료
2. 주어진 키 값이 현재 노드 키 값보다 작으면 node변수를 node->left로 변경
3. 주어진 키 값이 현재 노드 키 값보다 크면 node 변수를 node->right로 변경
4. while문 반복이 종료되었는데도 아직 함수가 return 되지 않았다면 key == node->key의 if문에
걸리지 않은 것, 즉 탐색이 실패한 것이므로 NULL을 반환한다.
*반복적인 탐색연산이 순환적인 탐색연산보다 효율성 측면에서 우수하다.
TreeNode *search_itr(TreeNode *node, int key){
while(node != NULL){
if(key==node->key) return node;
else if(key<node->key){
node = node->left;
}
else{
node = node->right;
}
}
return NULL;
}
● 이진탐색트리에서 삽입연산
삽입연산 이전에 탐색 연산을 수행하여야 한다.
1. 같은 키값을 갖는 노드가 없어야 하고
2. 탐색에서 실패한 지점이 이후 우리가 삽입연산을 수행할 위치가 되기 때문
삽입연산은 항상 단말노드에서 수행된다. 새로운 노드는 단말 노드의 하위 노드로 추가된다.
TreeNode *new_node(int item){
TreeNode *temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
TreeNode *insert_node(TreeNode *node, int key){
if(node == NULL) return new_node(key);
if(key <node->key){
node->left = insert_node(node->left,key);
}
else if(key > node->key){
node->right = insert_node(node->right,key);
}
return node;
}
● 이진탐색트리에서 삭제연산
삭제하려는 노드가 트리의 어디에 위치하는 지를 알기 위해 탐색연산부터 수행한다.
다음과 같은 3가지 경우를 고려한다.
CASE1: 삭제하려는 노드가 단말 노드
CASE2: 삭제하려는 노드가 왼쪽 또는 오른쪽 서브 트리 중 하나만 가지고 있는 경우
CASE3: 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
●CASE1: 삭제하려는 노드가 단말 노드
- 부모노드를 찾아서 부모노드 안의 링크필드를 NULL로 만들어 연결을 끊는다.
●CASE2: 삭제하려는 노드가 왼쪽 또는 오른쪽 서브 트리 중 하나만 가지고 있는 경우
- 자식 노드를 부모 노드에 붙여주고 삭제하려는 자기 노드는 삭제한다.
●CASE3: 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
- 왼쪽 서브트리의 가장 오른쪽에 있는 노드 또는 오른쪽 서브트리의 가장 왼쪽에 있는 노드를 찾아서
부모 노드에 붙여주고 삭제하려는 자기 노드는 삭제한다.
TreeNode * min_value_node(TreeNode *node){
TreeNode *current = node;
while(current->left !=NULL){
current = current->left;
}
return current;
} // 파란글씨, 오른쪽 트리의 가장 왼쪽 노드를 찾기 위함
전체 코드는 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
typedef int element;
typedef struct TreeNode{
element key;
struct TreeNode *left, *right;
int is_thread;
}TreeNode;
TreeNode *search(TreeNode * node, int key){
if(node ==NULL) return NULL;
if(key == node->key) return node;
else if(key < node->key){
return search(node->left,key);
}
else{
return search(node->right,key);
}
}
TreeNode *search_itr(TreeNode *node, int key){
while(node != NULL){
if(key==node->key) return node;
else if(key<node->key){
node = node->left;
}
else{
node = node->right;
}
}
return NULL;
}
TreeNode *new_node(int item){
TreeNode *temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
TreeNode *insert_node(TreeNode *node, int key){
if(node == NULL) return new_node(key);
if(key <node->key){
node->left = insert_node(node->left,key);
}
else if(key > node->key){
node->right = insert_node(node->right,key);
}
return node;
}
TreeNode * min_value_node(TreeNode *node){
TreeNode *current = node;
while(current->left !=NULL){
current = current->left;
}
return current;
}
TreeNode *delete_node(TreeNode *root, int key){
if(root ==NULL) return root;
if(key< root->key){
root->left = delete_node(root->left,key);
}
else if (key>root->key){
root->right = delete_node(root->right,key);
}
else{
if(root->left ==NULL){ // CASE1 or CASE2
TreeNode * temp = root->right;
free(root);
return temp;
}
else if(root->right ==NULL){
TreeNode *temp = root->left;
free(root);
return temp;
}
//CASE3
TreeNode *temp = min_value_node(root->right);
root->key = temp ->key;
root->right = delete_node(root->right,temp->key);
}
return root;
}
void inorder(TreeNode *root){
if(root){
inorder(root->left);
printf("[%d] ",root->key);
inorder(root->right);
}
}
int main(){
TreeNode * root = NULL;
TreeNode *temp = NULL;
root = insert_node(root,30);
root = insert_node(root,20);
root = insert_node(root,10);
root = insert_node(root,40);
root = insert_node(root,50);
root = insert_node(root,60);
printf("이진 탐색 트리 중위 순회 결과 \n");
inorder(root);
printf("\n");
if(search(root,30)!=NULL){
printf("트리에 30이 있음\n");
}
else{
printf("트리에 30이 없음\n");
}
return 0;
}
● 이진탐색트리의 분석
탐색, 삽입 삭제 연산의 평균적인 시간 복잡도: 트리의 높이가 h일 때 O(h),
n개의 노드를 가지는 이진 탐색 트리의 경우 일반적인 트리의 높이가 ⌈log2(n)⌉ 이므로 O(log2n)
최악의 경우: 한쪽으로 치우친 경사 트리가 되면 트리의 높이는 n이기 때문에 O(n)이 되어
선형 탐색과 같은 시간 복잡도를 가진다.
따라서 트리의 높이를 ⌈log2(n)⌉로 만들기 위해 트리를 균형지게 만드는 다양한 기법들이 있다.
균형 트리는 12장에서 다룬다.
♠ 310p Quiz
01 ⌈log2(9)⌉ = 4
02 17 14 01 26 66 28 34 80
03 26
/ \
14 28
/ \
02 66
/ \
34 80
8.12 이진 탐색 트리의 응용: 영어 사전
기존 이진 탐색 트리 코드에서 구조체를 키로 사용하는 것 외에 큰 차이점이 없어서 생략
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter9. 우선순위 큐 (1) (0) | 2023.12.01 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 8강 (2) | 2023.11.30 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter8. 트리 (1) (2) | 2023.11.25 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 7강 (1) | 2023.11.23 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter7. 연결 리스트 II (2) (0) | 2023.11.22 |
