9.1 우선순위 큐 추상 데이터 타입
● 우선순위 큐: 우선순위의 개념을 큐에 도입한 자료구조로, 우선순위가 높은 데이터가 먼저 나간다.
| 자료구조 | 삭제되는 요소 |
| 스택 | 가장 최근에 들어온 데이터 |
| 큐 | 가장 먼저 들어온 데이터 |
| 우선순위 큐 | 가장 우선순위가 높은 데이터 |
- 우선순위 큐는 배열, 연결 리스트 등의 여러 방법으로 구현이 가능한데, 가장 효율적인 구조는 heap이다.
- 최소 우선순위 큐는 가장 우선 순위가 낮은 요소를, 최대 우선순위 큐는 우선 순위가 높은 요소를 먼저 삭제한다.
♠ 324p Quiz
01 가장 최근에 들어온 데이터에 우선순위를 부여하면 스택을, 가장 먼저 들어온 데이터에 우선순위를 부여하면
큐를 구현할 수 있는 등 적절한 우선순위만 부여하면 여러 일반적인 자료구조를 구현할 수 있기 때문
02 01에서 답함
9.2 우선순위 큐의 구현 방법
● 배열을 사용하는 방법
CASE1: 정렬 되어 있지 않은 배열
- 삽입: 배열의 맨 끝에 새로운 요소 추가, O(1)
- 삭제: 우선순위가 높은 요소를 찾아야 하기에 탐색 후 삭제, 삭제 후 뒷 요소들을 앞으로 전체 이동, O(n)
CASE2: 정렬 되어 있는 배열
- 삽입: 순차탐색이나 이진탐색 등 삽입할 위치를 찾은 후 삽입 위치 뒷 요소들을 전체 이동 후 삽입, O(n)
- 삭제: 숫자가 높은 것이 우선순위가 높다고 가정하면 맨 뒷 요소를 삭제, O(1)
● 연결 리스트를 사용하는 방법
CASE1: 정렬 되어 있지 않은 연결 리스트
- 삽입: 첫 번째 노드로 새로운 요소 추가, O(1)
- 삭제: 우선순위가 높은 요소를 찾아야 하기에 탐색 후 삭제, O(n)
CASE2: 정렬 되어 있는 연결 리스트
- 삽입: 우선순위가 높은 요소를 찾아야 하기에 탐색 후 삽입, O(n)
- 삭제: 첫 번째 노드를 삭제, O(1)
● 히프를 사용하는 방법
히프: 완전 이진 트리의 일종으로 우선순위 큐를 위하여 특별히 만들어진 자료구조.
- 일종의 느슨한 정렬 상태[완전히 정렬된 것은 아니지만 전혀 정렬이 안된 것도 아닌 상태] 유지
- 히프의 효율은 O(log2n)으로, 다른 방법들보다 상당히 유리
| 표현 방법 | 삽입 | 삭제 |
| 순서 없는 배열 | O(1) | O(n) |
| 순서 없는 연결 리스트 | O(1) | O(n) |
| 정렬된 배열 | O(n) | O(1) |
| 정렬된 연결 리스트 | O(n) | O(1) |
| 히프 | O(logn) | O(logn) |
9.3 히프
● 히프의 개념
히프(head): 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리
- '더미'와 비슷한 자료구조, 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아낸다.
- key(부모노드) ≥ key( 자식노드)
- 완전 이진 트리(complete binary tree)이다.
- 이진 탐색 트리와 달리 큰 값이 상위 레벨이 있고 작은 값이 하위 레벨이 있는 정도로만 정렬돼 있다.
- 히프의 목적은 삭제 연산이 수행될 때, 가장 큰 값(루트)을 찾아내기만 하면 되는 것이므로 전체를 정렬할 필요는 없다.
● 히프의 종류, 구현
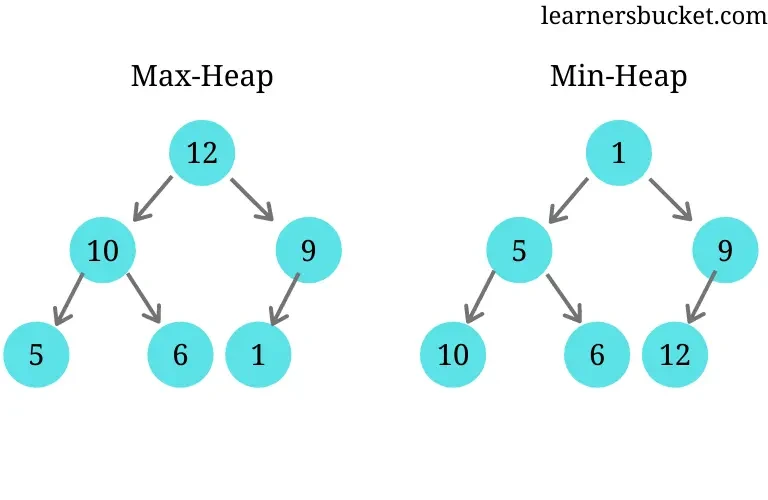
- 최대 히프(max-heap): 부모 노드의 키 값이 자식 노드보다 크거나 같은 완전 이진 트리
- 최소 히프(min-heap): 부모 노드의 키 값이 자식 노드보다 작거나 같은 완전 이진 트리
* 히프는 완전 이진 트리이기 때문에 각 노드에 완전 이진 트리에 대응되는 번호를 붙일 수 있다.
* 인덱스 0 은 사용하지 않는다.
[ 노드 i의 부모 노드 인덱스 = i/2, 노드 i의 왼쪽 자식 노드 인덱스 = 2i, 노드 i의 오른쪽 자식 노드 인덱스 = 2i+1]
9.4 히프의 구현
● 히프의 정의
typedef struct{
int key;
}element;
typedef struct{
element head[MAX_ELEMENT];
int heap_size;
}HeapType;히프의 각 요소들을 element로 정의하고, 히프를 element의 1차원 배열로 표현한다.
● 히프의 삽입
- 우선 새로운 노드를 히프의 마지막 노드로 삽입 후, 부모 노드들과 교환하여 히프의 성질을 만족시켜 준다.
- 실제 구현에서는 매번 부모 노드와 비교 후 자리를 교환하는 것이 아닌, 부모 노드만을 끌어내린 다음
삽입될 위치가 확정되면 새로운 노드를 해당 위치로 이동시킨다.
void insert_max_heap(HeapType *h, element item){
int i;
i = ++(h->heap_size);
while((i != 1)&&(item.key > h->heap[i/2].key)){//부모노드와 비교
h->heap[i] = h->heap[i/2];
i /=2;
}
h->heap[i] = item;
}
● 히프의 삭제
- 최대 히프에서 삭제 연산: 최댓값을 가진 루트 노드 삭제
- 루트 노드 삭제 후 히프의 마지막 노드를 루트 노드 자리에 가져온다.
- 그 후 새로운 루트 노드와 자식 노드들 중 큰 값과 크기를 비교해서 자식 노드가 더 크면 교환한다.
- 위를 최대 히프 성질에 만족할 때까지 반복한다.
element delete_max_heap(HeapType *h){
int parent, child;
element item, temp;
item = h->heap[1]; // 삭제할 노드는 루트노드
temp = h->heap[(h->heap_size)--];
parent =1;
child =2;
while(child <= h->heap_size){
if((child<h->heap_size)&&(h->heap[child].key < h->heap[child+1].key)){
child ++;
} // 왼쪽 자식 노드와 오른쪽 자식 노드 중 오른쪽 자식 노드가 크면 child 변경
if(temp.key>=h->heap[child].key) break; //최대 heap 만족하면 break
h->heap[parent] =h->heap[child];
parent = child;
child *=2;
}// whlie문을 빠져나오면 parent 위치가 확정됨
h->heap[parent] = temp;
return item;
}
● 히프의 복잡도 분석
- 삽입과 삭제 각각 최악의 경우 트리의 높이에 해당하는 연산이 필요하다.
- 히프가 완전 이진 트리이므로 높이는 log2n이 되고 삽입과 삭제의 시간 복잡도는 O(log2n)이다.
♠ 340p Quiz
01 12
/ \
11 8
/ \ / \
10 6 2 5
/ \
3 4
02 10
/ \
6 8
/ \ / \
4 3 2 5
9.5 히프 정렬
- 정렬되지 않은 1차원 배열 데이터를 차례대로 최대 히프에 추가한다.
- 한 번에 하나씩 요소를 히프에서 delete 하여 배열의 뒤쪽부터 저장하면 배열은 오름차순으로 정렬된다.
- n개의 요소는 O(nlog2n)시간 안에 정렬된다.
void heap_sort(element a[],int n){
HeapType *h;
h = create();
init(h);
for(int i =0;i<n;i++){
insert_max_heap(h,a[i]);
}// 최대 히프에 넣는다
for(int i= n-1;i>=0;i--){
a[i]=delete_max_heap(h);
}
free(h);
}
int main(){
element list[SIZE] = {23, 56, 11 ,9, 56, 99, 27, 34};
heap_sort(list,SIZE);
for(int i=0; i<SIZE;i++){
printf("%d ",list[i].key);
}
printf("\n");
return 0;
}
● 히프 정렬의 복잡도
- heap의 높이는 log2n이기에 하나의 요소에 대한 삽입 또는 삭제는 시간이 log2n만큼 소요된다.
- 요소의 개수가 n개이므로 전체적으로 O(nlog2n)의 시간이 걸린다.
- 히프 정렬이 최대로 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇 개만 필요할 때이다.
♠ 342p Quiz
01
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 200
#define SIZE 8
typedef struct{
int key;
}element;
typedef struct{
element heap[MAX_ELEMENT];
int heap_size;
}HeapType;
HeapType* create(){
return (HeapType*)malloc(sizeof(HeapType));
}
void init(HeapType *h){
h->heap_size=0;
}
void insert_min_heap(HeapType *h, element item){
int i;
i = ++(h->heap_size);
while((i != 1)&&(item.key < h->heap[i/2].key)){
h->heap[i] = h->heap[i/2];
i /=2;
}
h->heap[i] = item;
}
element delete_min_heap(HeapType *h){
int parent, child;
element item, temp;
item = h->heap[1]; // 삭제할 노드는 루트노드
temp = h->heap[(h->heap_size)--];
parent =1;
child =2;
while(child <= h->heap_size){
if((child<h->heap_size)&&(h->heap[child].key > h->heap[child+1].key)){
child ++;
}
if(temp.key<=h->heap[child].key) break; //최대 heap 만족하면 break
h->heap[parent] =h->heap[child];
parent = child;
child *=2;
}// whlie문을 빠져나오면 parent 위치가 확정됨
h->heap[parent] = temp;
return item;
}
void heap_sort(element a[],int n){
HeapType *h;
h = create();
init(h);
for(int i =0;i<n;i++){
insert_min_heap(h,a[i]);
}// 최대 히프에 넣는다
for(int i= n-1;i>=0;i--){
a[i]=delete_min_heap(h);
}
free(h);
}
int main(){
element list[SIZE] = {23, 56, 11 ,9, 56, 99, 27, 34};
heap_sort(list,SIZE);
for(int i=0; i<SIZE;i++){
printf("%d ",list[i].key);
}
printf("\n");
return 0;
}'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 9강 (1) | 2023.12.04 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] Chapter9. 우선순위 큐 (2) (1) | 2023.12.02 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 8강 (2) | 2023.11.30 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter8. 트리 (2) (1) | 2023.11.28 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter8. 트리 (1) (2) | 2023.11.25 |
