14.5 개방 주소법
● 충돌과 오버플로우
충돌: 서로 다른 키를 갖는 항목들이 같은 해시주소를 가지는 현상
오버플로우: 충돌이 발생했을 때 해당 해시 주소에 더 이상 빈 버킷이 남아있지 않아 항목을 저장할 수 없는 현상
오버플로우 해결하는 2가지 해결책
1. 개방주소법: 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장
2, 체이닝: 해시테이블의 하나의 위치가 여러 개의 항목을 저장할 수 있도록 해시테이블의 구조 변경
14.5절에서는 개방 주소법에 대해 다루고 14.6절에서 체이닝을 다룬다.
● 선형 조사법
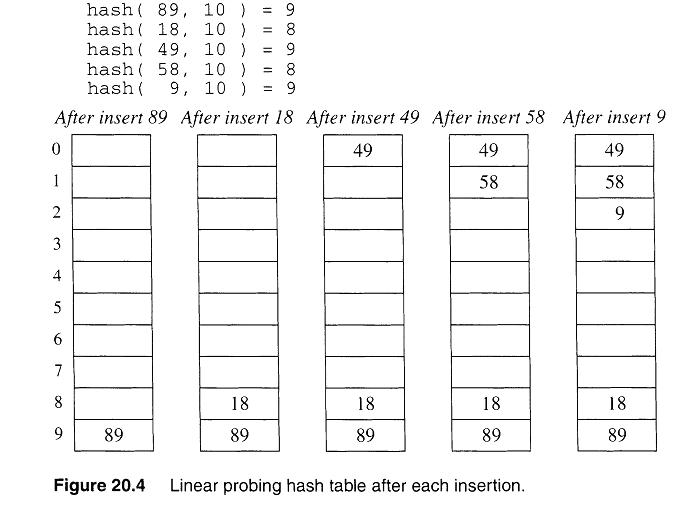
조사(probing): 해시테이블에서 비어있는 공간 찾기
선형조사법: ht[k]에서 충돌이 발생했다면 ht[k+1]이 비어있는지 확인 후 비어있다면 삽입, 비어있지 않다면 ht[k+2] 확인
조사를 시작했던 곳으로 돌아온다면 테이블은 가득찬 것으로 판단
ex) h(k) = k mod 7 함수를 크기가 7인 해시테이블에서 사용할 때 8, 1, 9, 6, 13 순으로 키 저장
h(8) = 1 → ht[1] = 8
h(1) = 1 → ht[1] 이미 참. (h(t)+1) mod 7 = 2 → ht[2] = 1
h(9) = 2 → ht[2] 이미 참. (h(t)+1) mod 7 = 3 → ht[3] = 9
h(6) = 6 → ht[6] = 6
h(13) = 6 → ht[6] 이미 참. (h(t)+1) mod 7 = 0 → ht[0] = 13
#define KEY_SIZE 10
#define TABLE_SIZE 13
typedef struct{
char key[KEY_SIZE];
}element;
element hash_table[TABLE_SIZE];
void init_table(element ht[]){
int i;
for(i=0; i<TABLE_SIZE; i++){
ht[i].key[0] NULL;
}
}
int transform(char *key){
int number = 0;
while(*key){
number +=(int)*key;
*key++;
}
return number;
}
int hash_function(char *key){
return transform(key) % TABLE_SIZE;
}- init_table()함수를 통해 키의 첫번째 문자가 NULL이면 버킷이 비어있는 것으로 생각하여 초기화
- transform()함수를 통해 문자열을 정수로 변환할 땐 '각 문자 아스키 코드를 합하여 변환'
- hash_function()함수를 통해 정수로 변환된 문자열을 테이블사이즈로 제산함수 적용
void hash_lp_add(element item, element ht[]){
int i,hash_value;
hash_value = i = hash_function(item.key);
while(!empty(ht[i])){
if(equal(item,ht[i])){
fprintf(stderr, "탐색키 중복\n");
exit(1);
}
i = (i+1)% TABLE_SIZE;
if(i==hash_value){
fprintf(stderr,"테이블 가득 참\n");
exit(1);
}
}
ht[i] = item;
}- empty() = 버킷이 비어있는지 검사 equal() = 두 개의 항목이 동일한지 검사
- 키에 대해서 해시 함수를 계산하여 hash_value에 저장
- 계산된 주소에 저장된 키와 현재 삽입하려는 키가 동일하면 중복
- 중복되지 않았다면 현재 주소를 나타내는 변수 i를 증가하여 다음 버킷을 가리키도록 함
- while문에 의해 ht[]가 비어있지 않고 i가 증가하다가 시작 주소로 되돌아온 경우에는
다른 모든 버킷이 가득 찬 상태이므로 더 이상 삽입 불가
void hash_lp_search(element item, element ht[]){
int i,hash_value;
hash_value = i = hash_function(item.key);
while(!empty(ht[i])){
if(equal(item, ht[i])){
fprintf(stderr,"탐색 %s: 위치 = %d\n",item.key,i);
return;
}
i = (i+1)% TABLE_SIZE;
if(i == hash_value){
fprintf(stderr,"찾는 값이 테이블에 없음\n");
return;
}
}
fprintf(stderr,"찾는 값이 테이블에 없음\n");
}- 삽입 함수와 마찬가지로 항목을 찾을 때까지 i 증가
void hash_lp_print(element ht[]){
int i;
printf("\n===============\n");
for(i=0; i<TABLE_SIZE; i++){
printf("[%d] %s\n",i, ht[i].key);
}
printf("=================\n\n");
}
int main(){
char *s[7] = {"do","for","if","case","else","return", "function"};
element e;
for(int i=0; i<7; i++){
strcpy(e.key,s[i]);
hash_lp_add(e,hash_table);
hash_lp_print(hash_table);
}
for(int i=0; i<7; i++){
strcpy(e.key,s[i]);
hash_lp_search(e,hash_table);
}
return 0;
}코드 완성
선형조사법
- 간단하게 구현
- 오버플로우가 자주 발생하면 집중과 결합에 의해 탐색의 효율 크게 저하
● 선형조사법의 삭제
- 항목 삭제 시 다른 항목도 탐색 불가능한 경우 발생
ex) h(k) = k mod 10 인 해시함수, 키가 5, 15 ,25 순으로 삽입 시 모두 충돌발생,
ht[5] = 5, ht[6] = 15, ht[7] = 25
이 상태에서 15 삭제 시 25를 탐색하려해도 ht[6]이 비어있어 탐색이 불가능해진다.
- 한 번도 사용 안 된 버킷과 사용되었으나 현재는 비어있는 버킷, 현재 사용중인 버킷으로 분류
- 한 번도 사용이 안 된 버킷을 만나야만 탐색 중단
연습문제 08 참고
● 이차 조사법: 선형 조사법과 유사하지만 조사할 위치가 아래와 같다.
(h(k) + inc*inc) mod M // for inc = 0, 1, ... , M-1
h(k), h(k) +1, h(k) +4, ...
- 테이블의 크기는 여전히 소수여야 함
- 선형조사법의 집중과 결합 문제를 크게 완화 가능
- 동일한 위치로 사상되는 여러 키들이 같은 순서에 의하여 빈 버킷을 조사하기에 2차 집중 발생
- 2차 집중은 이중 해싱법으로 해결
void hash_qp_add(element item, element ht[]){
int i,hash_value,inc =0;
hash_value = i = hash_function(item.key);
while(!empty(ht[i])){
if(equal(item,ht[i])){
fprintf(stderr, "탐색키 중복\n");
exit(1);
}
i = (hash_value + inc*inc)% TABLE_SIZE;
inc = inc +1;
if(i==hash_value && inc != 1){ // 교재와 달리 inc != 1 조건 필요
fprintf(stderr,"테이블 가득 참\n");
exit(1);
}
}
ht[i] = item;
}
● 이중 해싱법: 오버플로우가 발생함에 따라 항목을 저장할 다음 위치를 결정할 때, 별개의 해시 함수를 이용하는 방법
- 해시 테이블에 보다 균일하게 분포가능
- 선형 조사법 & 이차 조사법은 해시 함수값이 같으면 차후에 조사되는 위치도 같지만,
이중 해싱법에서는 키를 참조하여 더해지는 값이 새로이 결정되기에 2차집중을 피할 수 있다.
= 해시 함수값이 같아도 키가 다르면 서로 다른 조사 순서를 갖는다.
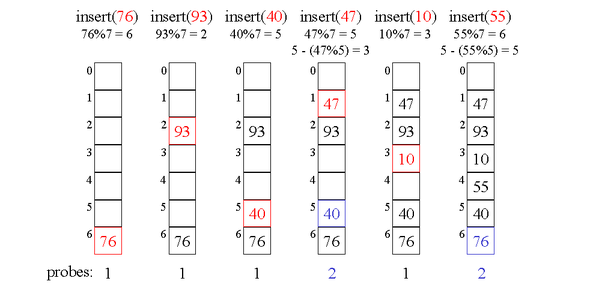
h'(k) = C - (k mod C) // [1..C] 사이의 값 생성 , C는 보통 M보다 약간 작은 소수
충돌 발생 시 조사하는 위치 h(k), h(k) + h'(k), h(k) + 2*h'(k), h(k) + 3*h'(k) ...
- 같은 버킷과 같은 탐색 순서를 가지는 요소가 거의 없어서 집중현상이 드묾
ex) h(k) = k mod 7, h'(k) = 5 - (k mod 5) M = 7 , C=5 (M보다 약간 작은 소수)
8, 1, 9, 6, 13 순으로 삽입시
1. h(8) = 8 mod 7 =1 → ht[1] = 8
2. h(1) = 1 mod 7 =1 충돌 발생 →(h(1) + h'(1)) mod 7 = 1+ (5 - (1 mod 5)) mod 7 = 5 → ht[5] = 1
3. h(9) = 9 mod 7 =2 → ht[2] = 9
4. h(6) = 6 mod 7 =6 → ht[6] = 6
5. h(13) = 13 mod 7 =6 충돌 발생 →(h(13) + h'(13)) mod 7 = 6 + (5 - (13 mod 5)) mod 7 = 1 충돌발생
→(h(13) + 2*h'(13)) mod 7 = (6+ 2*2) mod 7 = 3 → ht[3] = 13
5번에서 조사가 되는 인덱스는 6에서 시작하여 2씩 증가하는데, 6, 1, 3, 5, 0, 2, 4... 이렇게 테이블의 모든 위치를 조사한다.
*테이블 크기가 소수가 아니였으면 인덱스는 1, 3, 5, 1, 3, 5.. 이렇게 같은 위치만 조사한다.
14.6에 소개하는 체이닝은 아래 1, 2 번의 선형 조사법의 단점을 해결할 수 있다.
1. 한 번도 사용되지 않은 위치가 있어야만 탐색이 빨리 끝남
2. 거의 모든 위치가 사용되고 있거나, 사용된 적 있는 위치라면 실패하는 탐색일 때
테이블의 거의 모든 위치를 조사하여야 한다는 비효율성
14.6 체이닝
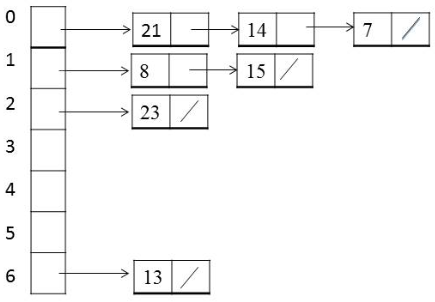
● 체이닝: 각 버킷에 고정된 슬롯을 할당하는 것이 아닌 연결 리스트를 할당하여 각 버킷이
하나 이상의 값을 저장하여 오버플로우 문제를 해결하는 방법
- 버킷 내에서 원하는 항목 찾을 때는 연결 리스트를 순차 탐색
- 키 삽입 시에는 키들의 중복을 허용한다면 연결 리스트의 처음에다 삽입하는 것이 능률적
#define TABLE_SIZE 7
typedef struct{
int key;
} element;
typedef struct list{
element item;
struct list *link;
}list;
list *hash_table[TABLE_SIZE];
int hash_function(int key){
return key % TABLE_SIZE;
}- hash_table은 list 구조체를 가리키는 포인터 배열
void hash_chain_add(element item, list *ht[]){
int hash_value = hash_function(item.key);
list *ptr;
list *node_before = NULL, *node = ht[hash_value];
for(;node;node_before = node, node = node->link){
if(node->item.key == item.key){
fprintf(stderr, "이미 탐색키가 저장되어 있음\n");
return;
}
}
ptr = (list *)malloc(sizeof(struct list));
ptr -> item = item;
ptr -> link = NULL;
if(node_before){
node_before->link = ptr;
}
else{
ht[hash_value] = ptr;
}
}
- list 노드를 동적 생성한 다음 키를 복사
- 동일한 키의 존재를 파악하기 위해 노드 포인터를 이동
- 동일한 키가 없으면 연결 리스트의 맨 끝에 새로운 키를 포함하는 새로운 노드를 연결
- 기존의 연결 리스트가 없으면 (node_before == NULL 이면) 해시테이블의 포인터에 새로운 노드 연결
- 각 키 값의 버킷에 해당하는 연결 리스트에서 독립적으로 삽입이나 탐색이 이루어짐
- 연결리스트로 필요한 공간을 동적할당하여 사용가능하기에 공간 사용 효율이 우수
- 오버플로우 발생 시 해당 버킷만 처리하므로 수행 시간 면에서도 우수
♠ 564p Quiz
01

14.7 해싱의 성능 분석
성공적인 탐색 → O(1)
실패한 탐색 → 충돌, 오버플로우 → O(1)보다 느려짐
해싱의 성능 분석
α = 적재 밀도(loading density) 또는 적재 비율(loading factor)
= 저장된 항목의 개수 / 해싱테이블의 버킷의 개수 = n / M
α의 최대값은 충돌 해결 방법에 따라 달라짐
· 선형조사법
- 해시 테이블이 다 차면 α = 1
- 실패한 탐색: 1/2 {1+ 1/(1-α)^2} 성공한 탐색: 1/2 {1+ 1/(1-α)} //탐색을 위한 비교 연산 수
| α | 실패한 탐색 | 성공한 탐색 |
| 0.1 | 1.1 | 1.1 |
| 0.3 | 1.5 | 1.2 |
| 0.5 | 2.5 | 1.5 |
| 0.7 | 6.1 | 2.2 |
| 0.9 | 50.5 | 5.5 |
- 테이블이 채워질 수록 충돌은 더 잦게 일어나기 때문에 적재밀도가 0.5를 넘지 않도록 해야 함
· 체인법
- 체인법에서는 저장할 수 있는 항목의 수가 테이블의 크기를 무한히 넘어설 수 있으므로 α는 최대값 가지지 않음
- α가 (항목의 개수 / 연결 리스트의 개수)이므로 평균적으로 하나의 연결 리스트 당 몇 개의 항목인가를 나타냄
- 실패한 탐색: α 성공한 탐색: 1+α/2
찾고자 하는 위치에 연결 리스트가 비어있으면 O(1)만에 탐색실패 -> 평균적으로는 α
연결 리스트에 항목이 존재할 것이고, 평균적으로 α의 항목을 비교하되 테이블에 존재하는 포인터까지 계산
| α | 실패 | 성공 |
| 0.1 | 0.1 | 1.1 |
| 0.3 | 0.3 | 1.2 |
| 0.5 | 0.5 | 1.3 |
| 0.7 | 0.7 | 1.4 |
| 0.9 | 0.9 | 1.5 |
| 1.3 | 1.3 | 1.7 |
| 1.5 | 1. | 1.8 |
| 2.0 | 2.0 | 2.0 |
- α가 증가하더라도 성능이 선형 조사법처럼 급격히 떨어지지는 않지만 효율성을 위해 α유지할 필요는 있음
* 제산 해시 함수와 함께 체이닝을 사용하는 방법이 우수하다는 연구 결과가 있다.
선형조사법: α 0.5 이하 유지
이차 조사법 & 이중 해싱법 : α 0.7 이하 유지
*선형주소법이 α가 작은 경우에는 이차 조사법이나 이중해싱보다 효율적일 수 있음
체인법: α에 비례하는 성능
● 해싱 vs 배열 이용 이진 탐색
- 해싱> 이진탐색
- 해싱은 이진탐색과 달리 삽입이 쉬움
- 이진 탐색 트리는 현재값보다 다음으로 큰, 다음으로 작은 값을 쉽게 찾음
- 이진 탐색 트리는 값의 크기순으로 순회하는 것이 쉬움
- 해싱은 순서가 없으며 초기에 얼마나 공간을 할당해야 하는지가 불명확
- 해싱의 최악의 시간 복잡도(하나의 버킷으로 키값이 집중되는 경우) O(n)을 가진다.
| 탐색방법 | 탐색 | 삽입 | 삭제 | |
| 순차탐색 | O(n) | O(1) | O(n) | |
| 이진탐색 | O(log2n) | O(log2n+n) | O(log2n+n) | |
| 이진탐색트리 | 균형트리 | O(log2n) | O(log2n) | O(log2n) |
| 경사트리 | O(n) | O(n) | O(n) | |
| 해싱 | 최선 | O(1) | O(1) | O(1) |
| 최악 | O(n) | O(n) | O(n) | |
14.8 해싱의 응용 분야
- 데이터 베이스 인덱싱
- 컴파일러에서 심볼 테이블 구현 시 심볼 테이블에서 해싱 사용
- 인터넷 검색 엔진
'CS > Data Structure' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] Chapter14. 해싱 (1) (0) | 2024.01.20 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 13강 (0) | 2024.01.20 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter13. 탐색 (2) (2) | 2024.01.13 |
| [C언어로 쉽게 풀어쓴 자료구조] Chapter13. 탐색 (1) (1) | 2024.01.08 |
| [C언어로 쉽게 풀어쓴 자료구조] 연습문제 12강 (1) | 2024.01.07 |
